Uhol

O priestorovom uhle pozri priestorový uhol.

Uhol alebo rovinný uhol je časť roviny určený dvoma polpriamkami so spoločným začiatkom.

Pomenovania

Polpriamky určujúce uhol v rovine sa volajú ramená uhla, spoločný bod ramien sa volá vrchol uhla. Množina bodov roviny vyseknutej uhlom sa nazýva vnútorné body uhla (vnútrajšok uhla), ostatné body z roviny voláme vonkajšie body uhla (vonkajšok uhla). Uhol sa znázorňuje pomocou ramien, medzi ktorými sa vyznačí oblúčikom vrchol uhla. Zápis vnútorného uhla sa vykonáva pomocou písmen gréckej abecedy napr. $\alpha$ , $\beta$ , $\gamma$ , vonkajší uhol sa označuje znakom vnútorného uhla s čiarkou $\alpha$ ', $\beta$ ', $\gamma$ '. Iným spôsobom označovania je pomocou symbolu uhla a troch bodov v poradí bod ramena – vrchol – bod na druhom ramene, napr. $\angle AVB$ .

Druhy uhlov

Nulový uhol je uhol, ktorého ramená ležia na sebe (všetky ich body sú totožné). Má presne 0°.
Ostrý uhol je uhol menší ako pravý uhol. Má viac ako 0° ale menej ako 90°.
Pravý uhol je polovica priameho uhla. Označujeme ho bodkou v oblúčiku, alebo hranatým "oblúčikom". Má presne 90°.
Tupý uhol je väčší ako pravý uhol. Má viac ako 90° ale menej ako 180°.
Priamy uhol je uhol, ktorého ramená sú navzájom opačné polpriamky, čiže spolu vytvárajú priamku. Má presne 180°.
Plný uhol je uhol, ktorého ramená sú totožné (ležia na sebe). Za uhol považujeme celú rovinu okolo nich. Je to doplnok nulového uhla v rovine. Má presne 360°.
Kosý uhol je uhol, ktorý nie je nulový, pravý, priamy ani plný (šikmý, nepriamy, nerovnobežný).
Dutý uhol je uhol, ktorý je menší ako priamy.

Konvexný uhol je uhol priamy, alebo menší než priamy
Konkávny uhol je väčší než priamy

Dvojice uhlov

Vrcholové uhly sú dva uhly, ktorých ramená sú opačné polpriamky. Vrcholové uhly sú zhodné.

Vedľajšie (susedné) uhly sú dva uhly, ktorých jedno rameno je spoločné a druhé ramená sú opačné polpriamky. Súčet vedľajších uhlov je priamy uhol, teda dva susedné uhly zvierajú 180°.

Súhlasné uhly sú dva uhly, ktorých prvé ramená ležia na jednej priamke a druhé ramená sú rovnobežné, pritom smer príslušných ramien je rovnaký (súhlasný). Súhlasné uhly sú zhodné.

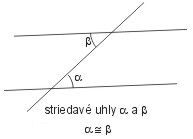
Striedavé uhly sú dva uhly, ktorých prvé ramená ležia na jednej priamke a druhé ramená sú rovnobežné, pritom smer príslušných ramien je opačný (striedavý). Striedavé uhly sú zhodné.

Súmernosť

Všetky uhly sú osovo súmerné, os uhla prechádza vrcholom a rozdeľuje uhol na dve zhodné časti (polovice uhla).

Orientovaný uhol

Orientovaným uhlom nazývame usporiadanú dvojicu polpriamok ${\vec {VA}}$ , ${\vec {VB}}$ so spoločným bodom $V$ , pričom polpriamku ${\vec {VA}}$ nazveme počiatočným ramenom uhla a polpriamku ${\vec {VB}}$ nazveme koncovým ramenom uhla. Bod $V$ je vrcholom orientovaného uhla.

Veľkosť uhla

Veľkosť uhla je nezáporné číslo, ktoré sa dá priradiť každému uhlu. Platí pritom, že zhodné uhly majú rovnakú veľkosť a tiež, že súčet veľkostí uhlov $\angle AVX$ a $\angle XVB$ je rovný veľkosti uhla $\angle AVB$ .

Číselná veľkosť uhla je daná voľbou nenulového uhla, ktorému priradíme veľkosť 1. V praxi sa pre meranie uhla používa

Oblúková (radiánová) miera

Hodnota jednotkového uhla v oblúkovej miere je zvolená tak, že uhol o veľkosti 1 vymedzuje na kružnici so stredom vo vrchole uhla oblúk, ktorého dĺžka je rovná polomeru danej kružnice. Hodnotu oblúkovej miery uhla $\alpha$ značíme $\operatorname {arc} \alpha$ .

Veľkosť ľubovoľného uhla je možné určiť ako pomer dĺžky oblúka vymedzeného ramenami na kružnici opísanej okolo vrcholu k polomeru tejto kružnice, tzn.

\alpha ={\frac {s}{r}}

,

kde $s$ je dĺžka kruhového oblúka medzi priamkami, ktoré vymedzujú uhol, a $r$ je polomer kruhového oblúka. Veľkosť pravého uhla je v oblúkovej miere rovná ${\frac {\pi }{2}}$ .

Uhlová jednotka oblúkovej miery je v radiánoch (skratka rad).

Stupňová miera

Stupňová miera je určená tak, že pravý uhol je rozdelený na 90 dielov, ktoré sa nazývajú (uhlové) stupne. Vzťah medzi stupňovou a oblúkovou mierou je možné zapísať ako

1° = π/180 rad

Uhlový stupeň sa delí na 60 (uhlových) minút, tzn. 1°=60′, a každá uhlová minúta sa delí na 60 (uhlových) sekúnd, tzn. 1′=60′′.

Stotinná miera

Stotinná miera je určená tak, že pravý uhol je rozdelený na 100 dielov, ktoré nazývame grady, gony alebo stotinné stupne. Vzťah medzi stotinnou a oblúkovou mierou je možné zapísať ako

1^{g}={\frac {\pi }{200}}rad

Vzťah medzi 100-tinnou a 60-tinnou (stupňovou) mierou vyjadruje

1^g = 9/10⁰ = 0,9⁰

1⁰ = 10/9 ^g

Ďalej pozri článok grad (uhol).

Príklady

Jeden stupeň je 1/180 priameho uhla, čiže priamy uhol má veľkosť 180°. Zlomky stupňov sa vyjadrujú buď v desiatkovej, alebo v šesťdesiatkovej sústave, pozri nasledujúce príklady:

pol stupňa = 0,5° = 0° 30’ t. j. 30 uhlových minút
osmina stupňa = 0,125° = 0° 7’ 30" t. j. 7 uhlových minút a 30 sekúnd.

Jeden radián je 1/π priameho uhla.

Veľkosť ďalších uhlov:

Nulový uhol: 0°, tzn. 0 rad
Ostrý uhol: medzi 0° a 90°, tzn. medzi 0 a π/2 rad
Pravý uhol: 90°, tzn. π/2
Tupý uhol: medzi 90° a 180°, tzn. π/2 a π rad
Kosý uhol: 0°<α<90° alebo 90°<α<180°
Dutý uhol: 0°<α<180°
Konvexný uhol: 0°≤α≤180°
Nekonvexný (vypuklý) uhol: medzi 180° a 360°, tzn. π a 2π rad
Priamy uhol: 180°, tzn. π rad
Plný uhol: 360°, tzn. 2π rad

Stupne sa používajú predovšetkým z historických dôvodov a tiež pre relatívne ľahké vykonávanie jednoduchých výpočtov. Radiány majú výhodu pri zložitejších výpočtoch – zvlášť pri derivovaní či integrácii nie je potrebné počítať so špeciálnymi konštantami. Radián je navyše relatívne intuitívna jednotka. Vyjadruje priamo dĺžku oblúka, vytýčeného daným uhlom na jednotkovej kružnici.

Veľkosť orientovaného uhla

Veľkosť orientovaného uhla je (v oblúkovej miere) rovná $\alpha +k2\pi$ , kde $\alpha$ je veľkosť rovnakého neorientovaného uhla a $k$ je celé číslo. Veľkosť orientovaného uhla je uhol, ktorým musí prejsť počiatočné rameno pri otočení do koncového ramena. Člen $k2\pi$ predstavuje počet celých otáčok okolo vrcholu uhla.

Operácie s uhlami

Sčítanie uhlov

Dva uhly sa sčítajú tak, že vezmete kružidlo a ľubovoľne ním pretnite uhol ktorý máte narysovaný, kružidlo zapichnite ne ľubovoľné miesto na dolnej čiare a prejdite čiarou k čiare 2.
Dole na uhla od čiary kružidla zapichnite kružidlo do dolnej čiary do miesta kde sa pretínajú čiary uhla a kružidla a druhý koniec kružidla na druhú čiaru kde sa pretína čiara uhla a kružidla a nechajte v kružidle veľkosť ktorú ste si z uhla vytiahli.
Ak máte 2 uhly na sčítanie nechajte si ešte stále veľkosť kružidla z prvého uhla a na druhom narysujte tak že ľubovoľne zapichnete kružidlo s veľkosťou z minulého uhla na čiaru druhého uhla a nakreslite oblúk na druhú čiaru a veľkosť na kružidle si o opäť ponechajte.
Narysujte čiaru s jedným bodom a kružidlo so stále rovnakou veľkosťou zapichnite do bodu (bod musí byť na ľavej strane) a narysujte kružidlom oblúk doľava.
Na oboch uhloch zanikli ramená tam kde sa pretína oblúk kružidla a uhol tak tam zapichnite kružidlo a nakreslite oblúk do druhého ramena. Nechajte si veľkosť a zapichnite kružidlo na narysovanú čiaru a na bode zapichnite a narysujte oblúk do predchádzajúceho oblúka od kružidla než sa stretnú a potom odtiaľ kde sa stretli pravítkom narysujte čiaru do bodu a to isté s druhým uhlom a na obrázku vidíte výsledok.

Odčítanie uhlov

Dva uhly sa odčítajú tak, že sa jedným ramenom priložia dovnútra seba a výsledný uhol vznikne medzi druhými dvoma ramenami. Výpočtovo stačí odčítať veľkosti uhlov.

Násobenie uhlov prirodzeným číslom

Násobenie uhla prirodzeným číslom sa vykonáva na opakované sčítanie toho istého uhla toľkokrát, koľko je dané prirodzené číslo. Číselne sa vynásobí veľkosť uhla daným prirodzeným číslom.

Delenie uhlov dvoma

Uhol sa delí dvoma zostrojením osi uhla. číselne sa vydelí veľkosť uhla dvoma. Konštrukčne nie je možné vykonať presné delenie všeobecného uhla troma, úloha je známa pod menom trisekcia uhla.

Operácie s orientovanými uhlami

Pri operáciách s orientovanými uhlami je nutné zohľadniť ich znamienka.

Ak teda k orientovanému uhlu $\alpha$ pripočítame orientovaný uhol $\beta$ , ktorý je však opačne orientovaný, je výsledok rovnaký ako by sme od neorientovaného uhla o rovnakej veľkosti ako má uhol $\alpha$ odčítali neorientovaný uhol o rovnakej veľkosti ako má uhol $\beta$ . Výsledkom takejto operácie je opäť orientovaný uhol, ktorý má rovnakú orientáciu ako $\alpha$ , ak $\alpha >\beta$ , má orientáciu ako uhol $\beta$ , ak $\alpha <\beta$ .

Meracie prístroje

Meranie a určovanie uhlov je v praxi veľmi dôležité. Využíva ich astronómia, geodézia a mnoho ďalších odborov. Preto sa tiež vyvinul rad meracích prístrojov.

uhlomer – najjednoduchšie meradlo – ide o polkruhovú dosku so stupnicou po obvode. Zložitějšie prístroje majú pohyblivé rameno.
Jakubova palica – jednoduchý stredoveký astronomický prístroj merajúca na princípe porovnávania strán trojuholníka
kvadrant, sextant, oktant – používané v navigácii
teodolit – základný prístroj používaný v geodézii na meranie a určovanie zvislých a vodorovných uhlov

Pozri aj

Iné projekty

Commons ponúka multimediálne súbory na tému uhly.

Externé odkazy

Stupňová a oblúková miera