Primov algoritmus

Primov algoritmus (známy aj ako Jarníkov algoritmus, Primov-Jarníkov algoritmus alebo aj DJP algoritmus) je v informatike greedy algoritmus hľadajúci minimálnu kostru ohodnoteného grafu. Nájde teda takú podmnožinu hrán grafu, ktorá tvorí strom obsahujúci všetky vrcholy pôvodného grafu a súčet ohodnotenia hrán z tejto množiny je minimálny. Algoritmus patrí medzi najefektívnejšie a najelegantnejšie implementovateľné algoritmy s týmto účelom. Prvýkrát algoritmus popísal český matematik Vojtěch Jarník roku 1930. V roku 1957 ho nezávisle na Jarníkovi popísal americký matematik a informatik Robert Clay Prim a potom ešte raz v roku 1959 tento algoritmus znovu objavil holandský informatik Edsger Wybe Dijkstra a na jeho základe vytvoril svoj Dijkstrov algoritmus na hľadanie najkratšej cesty v ohodnotenom grafe.

Popis

Algoritmus začína s jedným vrcholom a postupne pridáva ďalšie, čím zväčšuje veľkosť stromu dovtedy, kým neobsahuje všetky vrcholy.

• Vstup: súvislý ohodnotený graf G(V,E)
• Inicializácia: V' = {x}, kde x je ľubovoľný vrchol z V, E' = {}
• Opakuj, kým neplatí, že V'=V:
  • Vyber hranu (u,v) z E s minimálnou cenou tak, že u patrí V' a v nepatrí V'
  • Pridaj v do V', pridaj (u,v) do E'
• Výstup: T(V',E') je minimálna kostra grafu

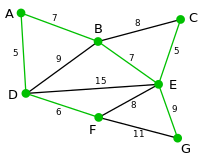
Príklad

Obrázok	Popis
	Toto je náš pôvodný ohodnotený graf. Čísla na okrajoch hrán označujú ich váhu.
	Z grafu vyberieme ľubovoľný vrchol. V tomto prípade vrchol D. Tým nám vznikne podgraf. Vrcholy A, B, E a F sú susednými vrcholmi D, teda sú s ním spojené hranou. Vrchol A je od vrcholu D vzdialený najmenej a bude vybraný ako druhý vrchol, spolu s hranou AD.
	Ďalším vybraným vrcholom bude vrchol, ktorý ma najmenšiu vzdialenosť od D alebo A. B má vzdialenosť od A 7 a od D 9. E je od D vzdialený 15 a F zase 6. Cena hrany DF je najnižšia, preto ako ďalší vrchol vyberieme F a ako hranu DF.
	Algoritmus pokračuje ako v predchádzajúcich krokoch. Vyberieme vrchol B, a hranu AB.
	V tomto prípade si môžeme vybrať medzi troma ešte nevybranými vrcholmi C, E a G. Spomedzi nich má E najmenšiu vzdialenosť od už vybraných vrcholov (7 od B). Preto vyberieme vrchol E a hranu BE.
	Jediné vrcholy prichádzajúce do úvahy sú C a G. C je vzdialený 5 od E a G je vzdialený 9 od E. Vyberieme C spolu s hranou EC.
	Vrchol G je jediný zvyšný vrchol. Od F má vzdialenosť 11, a od E 9. K E je bližšie, preto spolu s ním vyberieme aj hranu EG.
	Teraz sú už vybrané všetky vrcholy a teda sme získali minimálnu kostru grafu (vyznačená zelenou farbou). Celková váha kostry je 39.

Časová zložitost

Dátová štruktúra s ohodnotením hrán	Celková časová zložitosť
matica susednosti	O(n2)
binárna halda a zoznam susedov	O((n + m) log(n)) = n log(n)
Fibonacciho halda a zoznam susedov	O(m + n log(n))

Jednoduchá implementace s použitím reprezentace grafu pomocí matice sousednosti a prohledáváním pole cen má časovou složitost O(n²). S použitím binární haldy a seznamu sousedů dosáhneme složitosti O(m log n), kde m je počet hran a n je počet vrcholů. S použitím sofistikované Fibonacciho haldy složitost snížíme až na O(m + n log n), což je obzvláště rychlé u grafů, kde m je $\Omega (nlogn)$.