Hamiltonovský graf
Hamiltonovský graf je graf, ktorý obsahuje aspoň jednu hamiltonovskú kružnicu.
História[upraviť | upraviť zdroj]

V roku 1857 William Rowan Hamilton zostrojil matematický hlavolam, ktorého cieľom bolo nájsť takú uzavretú prechádzku po hranách pravidelného dvanásťstena, ktorá by obsahovala každý vrchol práve raz. Ak zabudneme na plochy dvanásťstena a nakreslíme jeho vrcholy a hrany v rovine, tak dostaneme graf nakreslený na obrázku:
Definícia Hamiltonovskej kružnice[upraviť | upraviť zdroj]
Hamiltonovská kružnica grafu je taká cesta, ktorá prejde práve raz všetky vrcholy grafu a skončí v počiatočnom vrchole.
Teda riešením Hamiltonovho hlavolamu je Hamiltonovská kružnica. Zistiť, či má graf uzavretý Eulerovský ťah, je ľahký problém, lebo stačí zistiť súvislosť grafu a paritu stupňov všetkých jeho vrcholov. Je prekvapujúce, že analogický problém pre Hamiltonovské kružnice je ťažký. Tento problém patrí do skupiny takzvaných NP-úplných problémov. Poznáme však veľmi veľa podmienok, ktorých splnenie vynucuje v grafe existenciu Hamiltonovskej kružnice. Jednu z najznámejších postačujúcich podmienok tohto typu dokázal nórsky matematik Øystein Ore v roku 1960 (1. podmienka).
Postačujúce podmienky[upraviť | upraviť zdroj]
- Nech G je graf, |V | = n, n ≥ 3. Ak pre každú dvojicu vrcholov, ktoré nie sú spojené hranou je súčet ich stupňov aspoň n, tak G je hamiltonovský.
- Nech G je graf, |V | = n, n ≥ 3. Ak má každý vrchol stupeň aspoň n/2, tak graf je hamiltonovský.
- Nech G je graf, |V | = n a predpokladajme, že n ≥ 3. Ak pre každé prirodzené číslo k < n/2 je počet vrcholov, ktorých stupeň neprevyšuje k, menší ako k, tak je graf hamiltonovský.
Nutná podmienka[upraviť | upraviť zdroj]
Symbolom c(G) označme počet komponentov grafu G.
Veta (nutná podmienka): Ak graf G = (V,E) je hamiltonovský, tak pre každú neprázdnu podmnožinu S množiny vrcholov V platí:
c(G - S) ≤ |S|
Príklad: Uvažujme graf G na obrázku č. 2. Môžeme si všimnúť, že S = {u1,u2,u3,u4,u5} je taká podmnožina množiny vrcholov grafu G, pre ktorú platí: c(G - S)= 6 > 5 = |S|, čiže neplatí nutná podmienka. To znamená že graf nie je hamiltonovský.
Príklady[upraviť | upraviť zdroj]
Príklady, kedy je graf hamiltonovský a kedy graf nie je.
- Prvý príklad
-
Obr.1
-
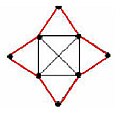
Obr.2
Hoci tento graf nespĺňa ani jednu z vyššie uvedených podmienok, je to hamiltonovský graf (ako vidno z obrázka 2), keďže existuje hamiltonovská kružnica nakreslená červenou farbou. Uvedené podmienky sú totiž iba postačujúcimi, ale nie nutnými podmienkami hamiltonovskych grafov.
- Druhý príklad
Graf na obrázku spĺňa všetky 3 podmienky:
- podmienku, lebo každý jeho vrchol má stupeň aspoň 3,
- podmienku, lebo každé dva vrcholy nespojené hranou majú súčet stupňov aspoň 6,
- podmienku, lebo v ňom nie sú žiadne vrcholy stupňa menšieho ako 3.
Literatúra[upraviť | upraviť zdroj]
- Vrba, A. Grafy pro III.ročník tříd gymnázií se zaměřením na matematiku, na matematiku a fyziku a pro seminář a cvičení z matematiky ve IV.ročníku gymnázií. Praha, SPN, 1989
- Nešetřil, J. Teorie grafů.Praha, SNTL, 1979
- Arnošt Večerka - Grafy a grafové algoritmy - skripta UPOL [1]