z Wikipédie, slobodnej encyklopédie
Moment zotrvačnosti  je fyzikálna veličina, ktorá vyplýva zo vzťahu
je fyzikálna veličina, ktorá vyplýva zo vzťahu

kde  je vzdialenosť infinitezimálne malého kúsku telesa s hmotnosťou
je vzdialenosť infinitezimálne malého kúsku telesa s hmotnosťou  od osi otáčania.
od osi otáčania.
| popis
|
tvar telesa
|
moment zotrvačnosti
|
poznámka
|
dutá valcová plocha bez dna a veka, s polomerom  a hmotnosťou a hmotnosťou 
|

|
 |
—
|
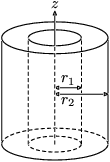
dutý hrubostenný valec bez dna a veka vnút. polomer  , vonk. polomer , vonk. polomer  , hmotnosť , hmotnosť 
|
|

![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m[3({r_{1}}^{2}+{r_{2}}^{2})+h^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5841114577aade103e9d517b516111c2ea07ab0d)
|
—
|
plný valec s polomerom  , výška , výška  a hmotnosť a hmotnosť 
|

|


|
—
|
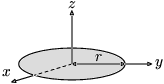
tenký disk s polomerom  a hmotnosťou a hmotnosťou 
|
|


|
—
|
plná guľa s polomerom  a hmotnosťou a hmotnosťou 
|

|
 |
—
|
dutá guľová plocha s polomerom  a hmotnosťou a hmotnosťou 
|

|
 |
—
|
kužeľ (pravouhlý) s polomerom  , výška , výška  hmotnosť hmotnosť 
|

|


|
—
|
plný kváder s výškou  , šírka , šírka  , dĺžka , dĺžka  , hmotnosťou , hmotnosťou 
|

|



|
pre podobne orientovanú kocku s dlžkou strany  a hmotnosťou a hmotnosťou  , ,  . .
|
tyč s dĺžkou  a hmotnosťou a hmotnosťou 
|

|

|
tento výraz je len teoretický približný vzorec a platí za predpokladu, že hmotnosť tyče je rozmiestnená vo forme nekonečne tenkej, avšak pevnej tyče
|
tyč s dĺžkou  a hmotnosťou a hmotnosťou 
|

|

|
tento výraz je len teoretický približný vzorec a platí za predpokladu, že hmotnosť tyče je rozmiestnená vo forme nekonečne tenkej, avšak pevnej tyče
|
Toroid s polomerom(veľký)  , polomer priereznej plochy(malý) , polomer priereznej plochy(malý)  a hmotnosťou a hmotnosťou  . .
|
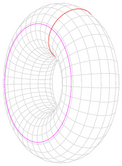 |
vzhľadom k vodorovnej osi:
vzhľadom k zvislej osi:
|
|
mnohouholník(plocha) s vrcholmi  , ,  , ,  , ..., , ...,  a hmotnosťou a hmotnosťou  . .
|

|

|
|






















![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m[3({r_{1}}^{2}+{r_{2}}^{2})+h^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5841114577aade103e9d517b516111c2ea07ab0d)



























