Perceptrón

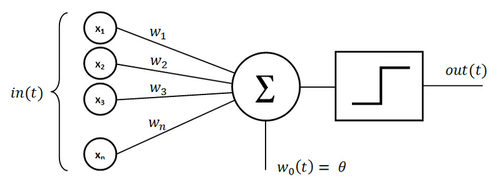
Perceptrón je špeciálnym prípadom formálneho neurónu predstavujúceho všeobecný výpočtový prvok všetkých neurónových sietí, v ktorom je vnútorný potenciál počítaný ako vážený súčet vstupov ,
a aktivačnou funkciou je sigmoida ,
,
kde je parameter strmosti (gain).[1]
Perceptrón bol navrhnutý Frankom Rosenblattom a je určený na dichotomickú klasifikáciu, tj. rozdelenie do dvoch tried, pri ktorých sa predpokladá, že triedy sú lineárne separovateľné v príkladovom priestore.[2]
Nech je daná množina vektorov x v n-rozmernom priestore. O každom z týchto vektorov vieme, že určite patrí do triedy1 alebo triedy2. Pod lineárnou separovateľnosťou dvoch tried rozumieme situáciu, keď existuje možnosť oddeliť objekty v príkladovom priestore pomocou nadroviny napr.: priamka v 2-rozmernom alebo rovina v 3-rozmernom priestore. Príklad lineárnej separovateľnosti v rovine je na obrázku [3]
História[4][upraviť | upraviť zdroj]
V r. 1943 McCulloch a Pitts predstavili prvý model neuronóvej siete. Aplikovali sieť zloženú z tzv. formálnych neurónov na symbolickú logiku, na výroky zložené z elementárnych logických operácií (x AND y, x OR y, NOT x). Model McCullocha a Pittsa nie je schopný učenia, jeho parametre (váhové a prahové koeficienty) sú pevne nastavené tak, aby model vykonával požadovanú Boolovu funkciu (logickú spojku alebo konjuktívnu klauzulu). Neurónové siete zostrojené z týchto neurónov sa neučia (neadaptujú) tak, aby vykonávali požadovanú Boolovu funkciu sa používajú neuróny s vopred danými požadovanými vlastnosťami.[5]
V r. 1958 Frank Rosenblatt ukázal, že McCullochove-Pittsove siete s modifikovateľnými synaptickými váhami sa dajú natrénovať tak, aby vedeli rozpoznávať a klasifikovať objekty. Vymyslel pre ne názov “perceptróny”. Hlavná myšlienka jeho trénovacej procedúry je takáto: najskôr zaznamenajme odpoveď každého formálneho neurónu na daný podnet. Ak je odpoveď správna, nemodifikujme váhy. Ak je odpoveď daného neurónu nesprávna, potom modifikujme váhy všetkých aktivovaných vstupných synapsií, a to nasledovným spôsobom: ak má byť neurón aktívny a nie je, zväčšime ich, a naopak, ak má byť na výstupe neurónu 0 a nie je, zmenšime ich.
V r. 1969 Minsky a Papert vo svojej knihe "Perceptróny: úvod do výpočtovej geometrie" poukázali na obmedzenia perceptrónov. Ukázali, že tieto siete vôbec nie sú výpočtovo univerzálne a nedokážu riešiť všetky triedy problémov. Hlavne však išlo o to, že perceptróny nedokážu riešiť tzv. lineárne neseparovateľné problémy. Klasickým najjednoduchším príkladom zlyhania je logická funkcia XOR (vylučujúce alebo).
V r. 1986 autori Rumelhart, Hinton a Williams zaviedli pravidlo učenia metódou spätného šírenia sa chýb pre viacvrstvové perceptróny (angl. error back-propagation learning). Formálne neuróny v ich perceptrónoch však už nie sú jednoduché logické prepínače McCullochovho-Pittsovho typu, ale analógové elementy so spojitou vstupno-výstupnou funkciou (najčastejšie sigmoidálneho tvaru).
Klasifikácia[6][upraviť | upraviť zdroj]
Perceptrón môže byť diskrétny alebo lineárny, rozdiel je v tom, akým spôsobom sa zo vstupných dát produkuje výstup.
- Diskrétny perceptrón má prahovanie: pokiaľ suma váhovaných vstupov neprekročí prah, tak na výstup pošle nulu (prípadne -1). Tým pádom je jasné, že diskrétny perceptrón pracuje nespojito – buď dá na výstup a, alebo b, ale nič medzi tým.
- Spojitý perceptrón nemá prahovaciu funkciu, výstup je spojitou funkciou sumy váhovaných vstupov. Ako aktivačná funkcia sa najčastejšie sa používa sigmoida, ale sú aj iné aktivačné funkcie. Dôležité vlastnosti aktivačnej funkcie sú, že sa dá derivovať, je ohraničená a monotónna.
Topológia[7][upraviť | upraviť zdroj]
Perceptrón, ktorý bol navrhnutý Rosenblattom ako jednoduchý diskrétny perceptrón so svojím učiacim algoritmom má tri vrstvy a to:
- senzorová vrstva
- asociatívna vrstva
- výstupný neurón
Spojenie medzi senzorovou vrstvou a asociatívnou má pevné váhy. Spojenie medzi asociatívnou vrstvou a výstupným neurónom je prepojené synapsiami s premenlivými váhami. Teda vstup do výstupného neurónu bol daný rovnicou
kde je počet neurónov v asociatívnej vrstve, sú váhy medzi asociatívnou vrstvou a výstupným neurónom, kde neurón "i" je v asociatívnej vrstve a na vstupe je "j-ty" prvok množiny , je stav "i"-teho neurónu a je prah. Výstup prechádza prahovaním v zmysle konečného výstupu
Je nutné poznamenať fakt, že jednoduchý perceptrón bol navrhnutý za cieľom klasifikácie do dvoch tried. V prípade elementárneho perceptrónu je separujúca nadrovina daná rovnicou
Z praktického hľadiska sa označuje vektor
,
vektor
kde je rozmer vektorov, teda počet neurónov v asociatívnej vrstve. Je potrebné poznamenať, že stále je a .
Učenie[6][upraviť | upraviť zdroj]
Neurónové siete sa učia, tj. pomocou nejakého pravidla učenia si upravujú svoje váhy. Podľa toho akým spôsobom prebieha učenie môžeme neurónové siete rozdeliť na
Perceptrón je zástupcom sietí v ktorých učenie prebieha s učiteľom. Základná myšlienka takéhoto upravovania váh je taká, že sa perceptrónu prezentuje nejaký vstup, a on vráti výstup. Získaný výstup sa porovná s očakávaný výstupom a vypočíta sa chyba, ktorú perceptrón spravil. Táto chyba sa potom použije na úpravu váh.
- Konkrétne pravidlo učenia v diskrétnom perceptróne je:
Kde je i-ta váha, je nejaký koeficient učenia, je želaný výstup a je získaný výstup, pričom je i-ty komponent vstupu.
- Učenie v spojitom perceptróne je komplikovanejšie. Všeobecne sa táto metóda nazýva gradient descent, pretože sa pre jej metaforické vyjadrenie používa predstava chybového priestoru, ktorý vyzerá ako lievik, na ktorého dne je optimálna (nulová) hodnota chyby. Gradient descent po tomto lieviku kráča tak, že sa snaží ísť stále smerom dolu, čo ho raz privedie na dno lievika. Toto je robené cez derivácie. Konkrétny vzorec učenia je:
Používa sa derivácia aktivačnej funkcie, pričom je želaný výstup, je získaný výstup a horné indexy znamenajú “pre daný pattern” (konkrétny vstup).
Referencie[upraviť | upraviť zdroj]
- ↑ Umělá inteligence (4) - prof. Ing. Vladimír Mařík, DrSc., prof. RNDr. Olga Štepánková, CSc., doc. Ind. Jiří Lažanský, CSc., a kolektív
- ↑ Center for Intelligent Technologies [online]. [Cit. 2007-11-15]. Dostupné online. Archivované 2007-11-17 z originálu.
- ↑ Neurónové siete Inžiniersky prístup (1. diel) - Peter Sinčák KKUI FEI TUKE: 2.4.1 Čo je to perceptrón? [online]. [Cit. 2013-12-13]. Dostupné online. Archivované 2011-08-28 z originálu.
- ↑ Úvod do teórie neurónových sietí - Vladimír Kvasnička, Ľubica Beňušková a kolektív
- ↑ Učebný text: FIIT STUBA
- ↑ a b Konekcionizmus - Perceptrón
- ↑ Neurónové siete Inžiniersky prístup (1. diel) - Peter Sinčák KKUI FEI TUKE: 2.4.2 Topológia perceptrónu? Archivované 2016-03-04 na Wayback Machine
Externé odkazy[upraviť | upraviť zdroj]
- FILIT – zdroj, z ktorého pôvodne čerpal tento článok.