Logaritmus

Logaritmus alebo logaritmická funkcia (pri základe a) je inverznou funkciou k exponenciálnej funkcii (s tým istým základom).
Logaritmom čísla x pri základe a teda nazývame v matematike také číslo y, pre ktoré platí:
a označujeme ho symbolicky
- ,
kde a > 0, a ≠ 1, x > 0. Funkciu
kde x > 0, potom nazývame logaritmickou funkciou so základom a. Definičný obor funkcie je interval , obor hodnôt tvoria všetky reálne čísla.
Funkcia je:
- klesajúca, ak
- rastúca, ak
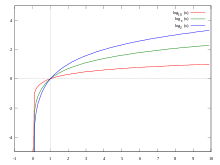
Graf logaritmickej funkcie nazývame logaritmická krivka; prechádza bodmi a .
Konštanta a sa nazýva základ logaritmu. Logaritmus o základe 10 sa nazýva dekadický logaritmus' (prípadne desiatkový, alebo Briggsov podľa matematika Henryho Briggsa). V prípade dekadického logaritmu sa v zápise vynecháva základ a zapisuje sa ako
Ďalším (v matematike pravdepodobne najpoužívanejším) prípadom je logaritmus o základe e (Eulerovo číslo). Tento sa nazýva prirodzený logaritmus (niekedy tiež Napierov podľa matematika Johna Napiera) a používa sa skrátený zápis
Hlavne v informatike sa objavuje logaritmus o základe 2, nazývaný binárny logaritmus, ktorý sa skrátene zapisuje:
Špeciálne základy[upraviť | upraviť zdroj]
Prirodzený logaritmus[upraviť | upraviť zdroj]
Prirodzený logaritmus alebo Napierov logaritmus (podľa Johna Napiera) je taký logaritmus, ktorý ma základ e (Eulerovo číslo).
Skrátený zápis:
Niekde sa môžete stretnúť aj so zápisom
alebo
Vlastnosti[upraviť | upraviť zdroj]
Pre platí:
- , kde






![{\displaystyle \left[1;0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5532acb1e1d1b1629a11706a392250009d52a3)
![{\displaystyle \left[a;1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc6fba7efd59a68a2c01caeb281dc0dfbed474c6)











