Parciálna derivácia
Parciálna derivácia funkcie o viacerých premenných je jej derivácia vzhľadom na jednu z týchto premenných, pričom s ostatnými narábame ako s konštantami (v tomto kontexte je teda opakom úplnej derivácie, kde môžu všetky premenné meniť svoje hodnoty). Parciálne derivácie sa využívajú vo vektorovom počte a v diferenciálnej geometrii.
Parciálna derivácia funkcie f vzhľadom na premennú x sa označuje f 'x, ∂xf, alebo ∂f/∂x. Symbol ∂, označujúci parciálnu deriváciu, je zaobleným písmenom d, ktorým sa zvykne označovať bežná derivácia. Označenie zaviedol Adrien-Marie Legendre, ale všeobecne sa začal uznávať, až po jeho oživení Carlom Gustavom Jacobom Jacobim.
Úvod[upraviť | upraviť zdroj]
Predpokladajme, že f je funkcia o viac ako jednej premennej, napríklad:
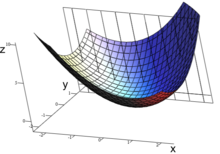

Je zložité určiť deriváciu takejto funkcie, keďže v každom bode tejto plochy existuje nekonečne veľa dotyčníc. Nájsť parciálnu deriváciu takejto funkcie vlastne znamená vybrať jednu z takýchto dotyčníc a určiť jej sklon. Zvyčajne nás najviac zaujíma dotyčnica, ktorá leží v rovine rovnobežnej so súradnicovou rovinou (y,z) alebo so súradnicovou rovinou (x,z). Dobrý spôsob, ako nájsť takéto dotyčnice je považovať ostatné premenné za konštanty. Napríklad, ak vo vyššie uvedenej funkcii hodláme nájsť dotyčnicu v bode (1, 1, 3), ktorá je rovnobežná s x-ovou osou, považujeme y za konštantu. Graf uvažovanej funkcie a jedna z prislúchajúcich rovín (y= 1) sú zobrazené na prvom obrázku. Na obrázku pod ním je rez grafom funkcie pre y= 1. Nájdením bežnej derivácie funkcie o jednej premennej, ktorá je zadaná vyššie uvedeným predpisom, pričom y považujeme za konštantu získame rovnicu požadovanej dotyčnice funkcie f rovnobežnej s osou x:
Teda v bode (1, 1, 3), je hodnota parciálnej derivácie (a teda aj tangens požadovanej dotyčnice) rovná 3 (tento poznatok získame substitúciou). Teda môžeme položiť, že
v bode (1, 1, 3).
Definícia[upraviť | upraviť zdroj]
Každú funkciu f o viacerých premenných môžeme interpretovať ako systém funkcií o jednej premennej, pričom funkcie indexujeme podľa ostatných premenných. Napríklad, ak vezmeme príklad uvažovaný v predchádzajúcej sekcii (a ako konštantu budeme tentoraz uvažovať premennú x), môžeme písať:
Inými slovami, každá hodnota x definuje funkciu označovanú fx, ktorá je funkciou jednej reálnej premennej. Teda,
Hneď ako zvolíme hodnotu x, napríklad nech x=a, potom f(x,y) určuje funkciu fa, ktorá každému y priraďuje hodnotu a2 + ay + y2:
V tomto výraze je a konštanta, nie premenná, preto fa je funkciou o jednej reálnej premennej, totiž y. Preto môžeme túto funkciu aj zderivovať ako funkciu jednej premennej, čím dostávame:
Tento postup je možné zopakovať pre ľubovoľnú hodnotu a. Ak z derivácií pre všetky možné hodnoty a vytvoríme opäť funkciu o dvoch premenných, dostávame:
Toto je parciálna derivácia funkcie f vzhľadom na y.
Vo všeobecnosti, parciálnu deriváciu funkcie f(x1,...,xn) vzhľadom na xi v bode (a1,...,an) teda je možné definovať ako:
V predchádzajúcom výraze sú všetky premenné okrem xi pevné a výber pevných hodnôt určuje funkciu o jednej reálnej premennej , pričom z definície máme
Príklad[upraviť | upraviť zdroj]

Objem kužeľa V závisí od jeho výšky h a polomeru podstavy r podľa nasledovného vzorca:
Parciálna derivácia V podľa r je
a vyjadruje mieru, akou sa mení objem kužeľa, ak meníme polomer jeho podstavy a výška ostáva konštantná. Naopak, parciálna derivácia V podľa h je
a vyjadruje mieru, akou sa mení objem kužeľa, ak meníme jeho výšku a polomer podstavy ostáva konštantný.
Parciálna primitívna funkcia[upraviť | upraviť zdroj]
Aj u parciálnych derivácií funkcií viacerých premenných existuje podobný koncept ako primitívna funkcia u bežných derivácií funkcií jednej reálnej premennej. Z parciálnej derivácie je teda možné čiastočne zrekonštruovať pôvodnú funkciu.
Uvažujme napríklad prvý príklad v tomto článku, .
Potom môžeme túto parciálnu deriváciu, ktorá je opäť funkciou dvoch premenných, "parciálne" zintegrovať podľa x, pričom y opäť považujeme za konštantu:
Je dôležité si uvedomiť, že integračná "konštanta" g(y) v tomto prípade nie je konštantou v pravom slova zmysle, ale funkciou všetkých premenných okrem x (v tomto prípade teda len y), ktoré sme pri procese integrovania považovali za konštanty. Dôvodom je, že pri procese parciálneho derivovania sme všetky premenné okrem x považovali za konštanty, a teda sa stratili všetky funkcie, ktoré nezáviseli od x. Najvšeobecnejší spôsob, ako sa s týmto faktom vyrovnať je teda ako integračnú "konštantu" použiť ľubovoľnú funkciu o všetkých premenných okrem x.
Systém funkcií , kde g je funkcia o jednej premennej y, teda pozostáva z práve všetkých funkcií, ktorých parciálna derivácia podľa x je .
Ak máme všetky parciálne derivácie nejakej funkcie (teda gradient), potom je možné z parciálnych primitívnych funkcií získaných uvedeným procesom úplne zrekonštruovať pôvodnú funkciu (až na konštantu).
Externé odkazy[upraviť | upraviť zdroj]
- Parciálna derivácia - projekt MathWorld (po anglicky)
Zdroj[upraviť | upraviť zdroj]
Tento článok je čiastočný alebo úplný preklad článku Partial derivative na anglickej Wikipédii.

















