Guľa (matematika)

Drôtený model trojrozmernej gule

Guľa alebo presnejšie uzavretá guľa je množina všetkých bodov euklidovského priestoru, ktorých vzdialenosť od pevného bodu (t.j. od tzv. stredu gule) nie je väčšia ako pevné reálne kladné číslo (t.j. ako tzv. polomer gule). Množina spomínaných bodov, ktorých vzdialenosť od pevného bodu je práve rovná spomínanému pevnému reálnemu kladnému číslu, sa volá guľová plocha (iné názvy: hranica gule, sféra, sférická plocha). Uzavretá guľa je teda inými slovami priestorové teleso "ukončené" guľovou plochou. Otvorená guľa alebo vnútro gule je uzavretá guľa bez guľovej plochy.

V topológii znamená n-rozmerná guľa (obvykle sa značí $B_n$) topologický priestor, ktorý je homeomorfný s n-rozmernou guľou v euklidovskom priestore $\mathbb{R}^n$.

Objem a povrch všeobecnej gule v euklidovskom priestore

N-rozmerná guľa s polomerom r v euklidovskom priestore $\mathbb{R}^n$ má objem (presnejšie, n-rozmernú Lebesguovu mieru) určený vzorcom

$V_{nD} = \frac{\pi^{\frac{n}{2}}}{\Gamma(1+\frac{n}{2})} r^n$

alebo tiež

$V_{nD} = \begin{cases} \left ( \frac{n}{2}! \right )^{-1} \pi^{\frac{n}{2}} r^n, & \mbox{pre }n\mbox{ parne} \\ \frac{2^{\frac{n+1}{2}}}{n!!} \pi^{\frac{n-1}{2}} r^n, & \mbox{pre }n\mbox{ neparne} \end{cases}$

kde $\Gamma(1+n/2)$ je prirodzené zobecnenie výrazu $(n/2)!$ pre nepárne n (pozri Gama funkcia) a n!! je dvojitý faktoriál. Je zaujímavé, že jednotková guľa (t. j. guľa s polomerom jedna) má najväčší objem v dimenzii n=5 a vo vyšších dimenziach sa jej objem limitne blíži k nule.

Povrch n-rozmernej gule tvorí (n-1)-rozmernú sféru (pozri sféra). Veľkosť jej povrchu (t. j. jej (n-1)-rozmerný objem, presnejšie, (n-1)-rozmerná Hausdorfova miera) je

$S_{nD} = n\frac{\pi^{\frac{n}{2}}}{\Gamma(1+\frac{n}{2})} r^{n-1}$

alebo

$S_{nD} = \begin{cases} n\left ( \frac{n}{2}!\right )^{-1}\pi^{\frac{n}{2}}r^{n-1}, & \mbox{pre }n\mbox{ parne} \\ 2^{\frac{n+1}{2}}\frac{n}{(n!!)}\pi^{\frac{n-1}{2}}r^{n-1}, & \mbox{pre }n\mbox{ neparne} \end{cases}$

Všeobecne pre n rozmernú guľu platí:

$S_{nD}(r) = \frac{\mathrm{d}V_{nD}}{\mathrm{d}r} = V_{nD}'(r) = n\frac{V_{nD}(r)}{r}$

Vzorce pre 3-rozmernú guľu

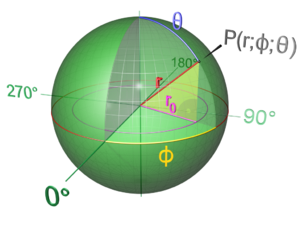
3-rozmerná guľa a jej koordináty

Nasledujúce vzorce popisujú trojrozmernú guľu v $\mathbb{R}^3$

Vzorce pre guľu
Obvod (najväčší)	$U \, = \, 2 \pi r$
Povrch	$A_O \, = \frac{\mathrm{d}V}{\mathrm{d}r} \, = \, 4 \pi r^2$
Objem	$V \, = \, \frac{4}{3} \pi r^3$
Projekčná plocha (plocha tieňa)	$A_{PF} \, = \, \pi r^2$
Objem guľového výseku	$V_{KS} \, = \, \frac{h^2 \pi}{3} (3r - h)$
Povrch guľového segmentu	$A_{KK} \, = \, 2 r h \pi = 2 r^2 \pi \left(1-\cos\frac{\alpha}{2}\right)$
Polomer gule	$r\,$
Výška guľového segmentu	$h \,$
Moment zotrvačnosti (os prechádza cez stred gule)	$J \, = \, \frac{2}{5} mr^2$
Steradián	$\alpha\,$

Pozri aj

• kruh
• elipsoid
• teleso

Iné projekty

Wikicitáty

• Wikicitáty ponúka citáty od alebo o Guľa (matematika)