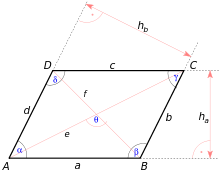
Rovnobežník

Rovnobežník

Rovnobežník je štvoruholník, ktorého protiľahlé strany sú rovnobežné a majú rovnakú dĺžku. Súčet susedných uhlov je 180°.

Vlastnosti

Rovnobežník má 4 strany, 4 vrcholy, 4 uhly, ktorých súčet je $2\pi$ (360°). Z rovnobežnosti protiľahlých strán vyplýva, že veľkosť protiľahlých strán je rovnaká, tzn.

$a=|AB|=|CD|=c,\qquad d=|AD|=|BC|=b.$

Z toho vyplýva, že aj veľkosť protiľahlých uhlov má rovnakú veľkosť, tzn.

$\alpha =\angle DAB=\angle BCD=\gamma ,\qquad \beta =\angle ABC=\angle CDA=\delta .$

Pretože $\alpha +\beta +\gamma +\delta =2(\alpha +\beta )=2\pi$, platí

$\alpha =\pi -\beta .$

Všeobecne má rovnobežník rôznu veľkosť priľahlých strán, t. j. $a\neq b$, a uhly rôzne od pravých uhlov, t. j. $\alpha \neq \beta$. Ak sú priľahlé strany rovnako veľké, t. j. $a=b=c=d$, nazývame taký rovnobežník kosoštvorcom. Ak sú uhly pravé, t. j. $\alpha =\beta =\gamma =\delta =\pi /2$, nazývame taký rovnobežník obdĺžnikom. Rovnobežník, ktorý je kosoštvorcom a obdĺžnikom zároveň nazývame štvorcom.

Uhlopriečky rovnobežníka sa vzájomne rozpoľujú. Dĺžky uhlopriečok sú:

$e=|AC|={\sqrt {a^{2}+d^{2}+2ad\cos \alpha }}={\sqrt {(a+h_{a}{\mbox{cotg}}\,\alpha )^{2}+h_{a}^{2}}}\,,$

$f=|BD|={\sqrt {a^{2}+d^{2}-2ad\cos \alpha }}={\sqrt {(a-h_{a}{\mbox{cotg}}\,\alpha )^{2}+h_{a}^{2}}}\,.$

Obsah

Obsah rovnobežníka je rovný:

$S=ah_{a}=bh_{b}=ab\sin \alpha$,

kde $a=|AB|$ a $b=|AD|$ sú dĺžky priľahlých strán rovnobežníka a $h_{a}$ je výška k strane $AB$, obdobne $h_{b}$ je výška k strane $AD$, $\alpha$ je vnútorný uhol medzi priľahlými stranami.

V rovine

Ak sú vrcholy $A,B,C,D$ zadané pomocou súradníc v rovine, t. j. $A=(x_{A},y_{A})$, $B=(x_{B},y_{B})$, atď, je obsah rovnobežníka rovný absolútnej hodnote determinantu zostaveného zo súradníc ľubovoľných troch vrcholov takto:

$S=\left|\det \left({\begin{array}{cc}x_{B}-x_{A}&x_{D}-x_{A}\\y_{B}-y_{A}&y_{D}-y_{A}\end{array}}\right)\right|=|(x_{B}y_{D}-x_{D}y_{B})-(x_{A}y_{D}-x_{D}y_{A})+(x_{A}y_{B}-x_{B}y_{A})|.$

Ak stotožníme, pre jednoduchosť, vrchol $A$ s počiatkom súradnicového systému, t. j. $A=(0,0)$, potom teda:

$S=|x_{B}y_{D}-x_{D}y_{B}|.$

Úplne analogicky možno spočítať objem ľubovolného kvádru, resp. nadobjem ľubovolného $n$ – rozmerného nadrovnobežnostenu (v $n$ – rozmernom priestore).

V trojrozmernom priestore

Ak sú vrcholy $A,B,C,D$ zadané pomocou súradníc v priestore, t. j. $A=(x_{A},y_{A},z_{A})$, $B=(x_{B},y_{B},z_{B})$, atď, a zavedieme ak stranové vektory

$\mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},z_{B}-z_{A}),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},z_{D}-z_{A}),$

je obsah rovnobežníka rovný euklidovskej norme (dĺžke) vektora $\mathbf {a} \times \mathbf {b}$, kde „$\times$“ značí vektorový súčin dvoch vektorov. Teda:

$S=\|\mathbf {a} \times \mathbf {b} \|_{2}={\Big (}(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {a} \times \mathbf {b} ){\Big )}^{1/2}$

kde „$\,\cdot \,$“ značí skalárny súčin dvoch vektorov.

Ak majú smerové vektory nulové zložky v smere osi $z$, t. j.

$\mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},0),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},0),$

potom:

$\mathbf {a} \times \mathbf {b} ={\Big (}0,0,(x_{B}y_{D}-x_{D}y_{B})-(x_{A}y_{D}-x_{D}y_{A})+(x_{A}y_{B}-x_{B}y_{A}){\Big )},$

čím dostaneme práve vzťah na výpočet obsahu rovnobežníka v rovine.

Ak stotožníme, pre jednoduchosť, vrchol $A$ s počiatkom súradnicového systému, t. j. $A=(0,0,0)$, potom

$\mathbf {a} \times \mathbf {b} =(y_{B}z_{D}-y_{D}z_{B},x_{D}z_{B}-x_{B}z_{D},x_{B}y_{D}-x_{D}y_{B})$

vo všeobecnom prípade , respektíve:

$\mathbf {a} \times \mathbf {b} =(0,0,x_{B}y_{D}-x_{D}y_{B})$

v prípade, že smerové vektory majú navyše nulové zložky v smere osi $z$.

Zovšeobecnením vektorového súčinu do $n$ – rozmerného priestoru (ide o o súčin $(n-1)$ lineárne nezávislých vektorov dĺžky $n$, ktorého výsledkom je vektor kolmý na všetky predchádzajúce, tvoriace s nimi, v danom poradí, pravotočivou bázou) možno úplne analogicky spočítať nadobsah ľubovoľného $(n-1)$ – rozmerného nadrovnobežníka v $n$ – rozmernom priestore.

V n-rozmernom (reálnom) priestore

Ak je rovnobežník daný dvoma postrannými vektormi v všeobecnom reálnom $n$ – rozmernom priestore

$\mathbf {a} =(a_{1},a_{2},a_{3},\ldots ,a_{n}),\qquad \mathbf {b} =(b_{1},b_{2},b_{3},\ldots ,b_{n}),$

potom jeho obsah je daný vzťahom:

$S={\sqrt {\|\mathbf {a} \|_{2}^{2}\|\mathbf {b} \|_{2}^{2}-\langle \mathbf {a} ,\mathbf {b} \rangle ^{2}}}={\Big (}(\mathbf {a} \cdot \mathbf {a} )(\mathbf {b} \cdot \mathbf {b} )-(\mathbf {a} \cdot \mathbf {b} )^{2}{\Big )}^{1/2},$

kde „$\langle \,,\,\rangle$“, resp . „$\,\cdot \,$“ značí skalárny súčin dvoch vektorov.

dosadením:

$\mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},0,\ldots ,0),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},0,\ldots ,0),$

opäť dostávame známy vzťah pre obsah rovnobežníka v rovine.

Pozri aj

• Geometrický útvar
• Štvoruholník
• Kváder

Zdroj

Tento článok je čiastočný alebo úplný preklad článku Rovnoběžník na českej Wikipédii.