Tálesova veta


V geometrii Tálesova veta (pomenovaná podľa gréckeho filozofa Tálesa z Milétu) hovorí, že ak A, B, C sú body na kružnici, kde AC je priemer kružnice, potom uhol ABC je pravý uhol.
Dôkaz[upraviť | upraviť zdroj]

Pri dôkaze použijeme nasledovné tvrdenia:
- súčet vnútorných uhlov v trojuholníku sa rovná 180°,
- základňové uhly rovnoramenného trojuholníka sú rovnaké.
Nech je stred kružnice. Keďže platí , a sú rovnoramenné trojuholníky a na základe rovnosti základňových uhlov rovnoramenných trojuholníkov, a . Označme uhly a . Tri vnútorné uhly trojuholníka sú potom , a . Súčet vnútorných uhlov každého trojuholníka je 180°:
z toho vyplýva po úprave
- ,
čo bolo treba dokázať.
Zovšeobecnenie[upraviť | upraviť zdroj]
Tálesova veta je špeciálnym prípadom nasledovnej vety:
- Nech sú dané tri body , a na kružnici so stredom , potom uhol je dvakrát taký veľký ako uhol .
Dôkaz tejto vety je podobný ako dôkaz Tálesovej vety uvedený vyššie.
Aplikácie[upraviť | upraviť zdroj]
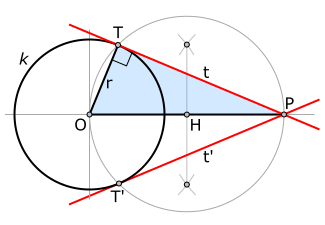
Tálesovu vetu môžeme použiť na konštrukciu dotyčnice danej kružnice, ktorá pretína daný bod (pozri obrázok). Nech je daná kružnica k so stredom O a vonkajší bod P mimo kružnice, chceme skonštruovať (na obrázku červenú) dotyčnicu (dotyčnice) kružnice k, ktorá pretína bod P. Označme bod, v ktorom sa (zatiaľ neznáma) dotyčnica t dotýka kružnice ako T. Zo symetrie je zrejmé, že polomer OT je kolmý na túto dotyčnicu. Nájdime stred H na úsečke spájajúcej body O a P a obkreslime kružnicu so stredom H cez tieto body. Podľa Tálesovej vety je hľadaný bod T priesečník tejto kružnice s danou kružnicou k, pretože to je bod na kružnici k, ktorý tvorí s bodmi O a P pravouhlý trojuholník OTP.
Pretože spomínané dve kružnice sa pretnú v dvoch bodoch, týmto spôsobom môžeme zostrojiť obe dotyčnice.
História[upraviť | upraviť zdroj]
Táles nebol prvý, ktorý formuloval túto vetu, keďže Egypťania aj Babylončania ju poznali, pravdepodobne empiricky, pretože sa nenašli žiadne dokumenty s jej dôkazom. Veta je pomenovaná po Tálesovi, ktorému sa pripisuje jej prvý dôkaz. Táles použil svoje vlastné výsledky o základňových uhloch rovnoramenného trojuholníka a súčte vnútorných uhlov v trojuholníku.


















