Kosínusová veta

V trigonometrii sa kosínusová veta používa na výpočet dĺžky strany, pričom poznáme veľkosť uhla ležiaceho oproti strane a dĺžku zvyšných dvoch strán (ktoré zvierajú tento uhol).

Kosínusová veta má tri základné varianty:

• a² = b² + c² - 2 × b × c × cos α
• b² = a² + c² - 2 × a × c × cos β
• c² = a² + b² - 2 × a × b × cos γ

Dôkaz

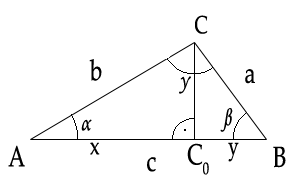
Nech v trojuholníku ABC päta výšky na stranu c rozdeľuje stranu c na dve časti:

• x = |AC₀|
• y = |C₀B|
• v_c = |CC₀|

Potom v trojuholníku AC₀C platí Pytagorova veta:

b² = v_c² + x²

v_c² = b² - x²

Obdobne v trojuholníku BC₀C platí Pytagorova veta:

a² = v_c² + y²

v_c² = a² - y²

Keďže strana c sa skladá z častí x a y, môžeme y vyjadriť ako y = c - x a teda y² = c² - 2cx + x². V trojuholníku AC₀C platí, že kosínus α je rovný pomeru strán x ku b. Z tohto vzťahu si teda môžeme vyjadriť x ako x = b × cos(α).

Na základe predchádzajúcich výpočtov vieme, že platí nasledujúca rovnosť:

v_c² = v_c²

b² - x² = a² - y²

b² - x² = a² - c² + 2cx - x²

b² = a² - c² + 2cx

b² = a² - c² + 2bc × cos(α)

a² = b² + c² - 2bc × cos(α)

Analogickým spôsobom môžeme dokázať aj zvyšné tvary kosínusovej vety.

Pozri aj

• Sínusová veta
• Tangentová veta
• Pytagorova veta
• Trigonometria