Zlatý rez
Zlatý rez, zlatý podiel alebo božský rez (lat. sectio divina) je iracionálne číslo s mnohými zaujímavými vlastnosťami. Geometrické tvary odvodené od tohto čísla sa v európskej kultúre považujú za esteticky veľmi príťažlivé a mnohé geometrické proporcie v prírode majú blízko k tomuto číslu.
Označuje sa gréckym písmenom φ (menej často aj gr. písmenom τ) a rovná sa približne 1,618034.
Definícia[upraviť | upraviť zdroj]
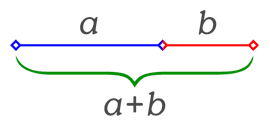
Číslo φ je odvodený od výsledku geometrickej úlohy ako rozdeliť (rozrezať) úsečku s dĺžkou x na dve časti a a b tak, aby pomer dĺžky dlhšej časti a ku kratšej časti b bol rovnaký ako pomer celej dĺžky x k dlhšej časti a. Tento pomer (x/a) je práve φ =1,618034, teda percentuálne dlhšia časť a tvorí cca 61,8% a kratšia b cca 38,2% x a pritom je aj pomer kratšej a dlhšej časti tiež 61,8% (38,2/61,8 = 61,8%).
Pomer možno vyrátať matematicky (a to viacerými spôsobmi napríklad pomocou Fibonacciho postupnosti) alebo geometricky.
Tu uvádzame len najjednoduchší matematický výpočet:
Keďže úsečka x sa skladá z častí a a b, môžeme dosadiť x = a + b a dostaneme:
Takže pre jednotlivé dĺžky x, a, b platí:
- (kratšia časť b krát φ rovná sa dlhšej časti a)
- (dlhšia časť a krát φ rovná sa súčtu častí)
Keď prvý vzťah dosadíme do druhého za člen a, dostaneme:
- respektíve
Z tohto vzťahu sa vykľuje kvadratická rovnica:
Po dosadení jednotkovej dĺžky menšej časti (b = 1) dostaneme:
Riešením kvadratickej rovnice sú dva korene:
Matematické vlastnosti[upraviť | upraviť zdroj]
Zaujímavý je aj vzťah koreňov rovnice, φ1 a φ2:
Číslo φ1 je tiež jediným kladným číslom, ktoré vyhovuje rovnici:
(Čo je zrejmé, pretože tak bolo vypočítané.)
Desatinný rozvoj[upraviť | upraviť zdroj]
Číslo φ rozvité na 1024 desatinných miest:
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 32265613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362 1076738937 6455606060 5922...
História[upraviť | upraviť zdroj]
| Tomuto článku alebo sekcii chýbajú odkazy na spoľahlivé zdroje, môže preto obsahovať informácie, ktoré je potrebné ešte overiť. Pomôžte Wikipédii a doplňte do článku citácie, odkazy na spoľahlivé zdroje. |
Mnohí odborníci premýšľajú o tom, od kedy ľudstvo pozná zlatý rez. Niektorí sa domnievajú, že stopy po zlatom reze možno badať napr. v Egyptských pyramídach. Je možné, že už Pythagoras alebo jeho žiaci boli so zlatým rezom oboznámení, keďže zlatý rez pravdepodobne používali pri konštrukcii pentagramu a aj iných geometrických útvarov. Prvý, kto jednoznačne definoval zlatý rez, bol Euklides vo svojom diele Základy okolo roku 300 p.n.l. Zlatý rez nazval ako "krajný a stredný pomer". V roku 1509 napísal Luca Pacioli svoje dielo Divina Proportione, ktoré skúma zlatý rez z pohľadu matematiky ale i umenia a metafyziky a bolo ilustrované samotným Leonardom da Vincim. Luca Pacioli vo svojom diele prevzal niektoré časti od maliara Piera della Francescu, ktorého obdivoval. Zlatý rez sa prekvapujúco objavuje v prírode, umení a matematike.