Konkávna funkcia: Rozdiel medzi revíziami
d robot Pridal: es:Función convexa |
štylistika, definície, obrázok, wikilinky |
||
| Riadok 1: | Riadok 1: | ||
[[Obrázok:Concave fnx.jpg|Graf funkcie konkávnej na intervale konkávnosti leží nad spojnicou krajných bodov tohto intervalu|thumb]] |
|||
'''Funkcia''' f(x) je '''konkávna''' na intervale [A,B], ak má táto [[funkcia]] [[dotyčnica|dotyčnicu]] na [[interval]]e [A,B], resp. v hraničných [[bod (geometria)|bodoch]] [A,B] má dotyčnice sprava alebo zľava, a ak pre každú dotyčnicu leží graf funkcie pod dotyčnicou. Inými slovami: |
|||
Spojitá konkávna funkcia na intervale <math>(a,b)</math>, je význačná tým, že jej graf leží pod každou jej zostrojenou dotyčnicou. Jednoduchou a názornou pomôckou môže byť predstava grafu konkávnej funkcie na <math>(a,b)</math> ako šálky, do ktorej nemožno naliať kávu, pretože sa vždy vyleje. Opačný prípad tvorí [[konvexná funkcia]]. Samotná definícia je analyticky odvodená z vlastností funkčných hodnôt konkávnej funkcie vzhľadom k spojnici krajných bodov intervalu konkávnosti. Možno povedať, že funkčné hodnoty konkávnej funkcie sú na intervale konkávnosti vždy nad spojnicou spomínaných krajných bodov. |
|||
*Ak funkcia f(x) je [[spojitá funkcia|spojitá]] na intervale [A,B] a má pre každý vnútorný bod intervalu [A, B] zápornú druhú [[derivácia|deriváciu]], potom je na intervale [A,B] konkávna. |
|||
*Funkcia je konkávna v intervale [A,B], ak jej [[graf]] je "otvorený nadol". |
|||
[[Obrázok:Concave fnx.jpg|left]] |
|||
<br clear="all"> |
|||
=== Didaktická pomôcka === |
|||
''Funkcia je v intervale [A,B] konkávna, ak sa do nádoby, ktorú v tomto intervale graf vykreslí, nedá naliať káva.'' |
|||
== |
==Definícia== |
||
[[Obrázok:Konkavna_konvexna_funkcia.PNG|Konkávna časť funkcie je vyznačená namodro. Graf na tomto intervale leží pod dotyčnicou. Zvyšná červená krivka označuje konvexnú časť a jej graf leží nad dotyčnicou|right|400px|thumb]] |
|||
| ⚫ | |||
Definíciu konkávnosti funkcie možno rozdeliť na definíciu konkávnosti funkcie a špeciálneho prípadu - rýdzej konkávnosti funkcie. Väčšinu elementárnych funkcií možno však považovať za rýdzo konkávne respektíve rýdzo konvexné. Príkladom môžu byť [[Polynóm|polynómy]]. |
|||
===Definícia rýdzo konkávnej funkcie=== |
|||
Nech ''f'' je funkcia spojitá na intervale <math>(a,b)</math>. Potom hovoríme, že funkcia ''f'' je na intervale <math>(a,b)</math> rýdzo konkávna práve vtedy, keď existuje číslo <math>\lambda\in(0,1)</math> s vlastnosťou<br /> |
|||
<center><math>\forall x,y\in(a,b),x<y:f(\lambda x+(1-\lambda)y)>\lambda f(x)+(1-\lambda)f(y)</math></center> |
|||
{{matematický výhonok}} |
|||
===Definícia konkávnej funkcie=== |
|||
Nech ''f'' je funkcia spojitá na intervale <math>(a,b)</math>. Potom hovoríme, že funkcia ''f'' je na intervale <math>(a,b)</math> konkávna práve vtedy, keď existuje číslo <math>\lambda\in(0,1)</math> s vlastnosťou<br /> |
|||
<center><math>\forall x,y\in(a,b),x<y:f(\lambda x+(1-\lambda)y)\geq\lambda f(x)+(1-\lambda)f(y)</math></center> |
|||
| ⚫ | |||
==Intervaly konkávnosti== |
|||
Pri hľadaní intervalov, na ktorých je funkcia konkávna sa postupuje použitím druhej derivácie funkcie. Intervaly konvexnosti a konkávnosti funkcie delia [[Inflexný bod|inflexné body]]. V týchto bodoch funkcia mení zakrivenie. Funkcia je preto rýdzo konkávna na intervale, kde <math>f''(x)<0</math>. Analogicky sa odvodí pravidlo pre interval konkávnej funkcie <math>f''(x)\leq0</math>. Daná derivácia musí existovať. To, že funkcia je diferencovateľná nevyplýva priamo z podmienky spojitosti skúmanej funkcie, preto treba pridať podmienku diferencovateľnosti. |
|||
==Pozri aj== |
|||
| ⚫ | |||
*[[inflexný bod]] |
|||
*[[extrém]] |
|||
| ⚫ | |||
[[cs:Konvexnost a konkávnost funkce]] |
[[cs:Konvexnost a konkávnost funkce]] |
||
Verzia z 16:20, 17. január 2009
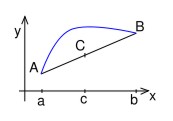
Spojitá konkávna funkcia na intervale , je význačná tým, že jej graf leží pod každou jej zostrojenou dotyčnicou. Jednoduchou a názornou pomôckou môže byť predstava grafu konkávnej funkcie na ako šálky, do ktorej nemožno naliať kávu, pretože sa vždy vyleje. Opačný prípad tvorí konvexná funkcia. Samotná definícia je analyticky odvodená z vlastností funkčných hodnôt konkávnej funkcie vzhľadom k spojnici krajných bodov intervalu konkávnosti. Možno povedať, že funkčné hodnoty konkávnej funkcie sú na intervale konkávnosti vždy nad spojnicou spomínaných krajných bodov.
Definícia

Definíciu konkávnosti funkcie možno rozdeliť na definíciu konkávnosti funkcie a špeciálneho prípadu - rýdzej konkávnosti funkcie. Väčšinu elementárnych funkcií možno však považovať za rýdzo konkávne respektíve rýdzo konvexné. Príkladom môžu byť polynómy.
Definícia rýdzo konkávnej funkcie
Nech f je funkcia spojitá na intervale . Potom hovoríme, že funkcia f je na intervale rýdzo konkávna práve vtedy, keď existuje číslo s vlastnosťou
Definícia konkávnej funkcie
Nech f je funkcia spojitá na intervale . Potom hovoríme, že funkcia f je na intervale konkávna práve vtedy, keď existuje číslo s vlastnosťou
Intervaly konkávnosti
Pri hľadaní intervalov, na ktorých je funkcia konkávna sa postupuje použitím druhej derivácie funkcie. Intervaly konvexnosti a konkávnosti funkcie delia inflexné body. V týchto bodoch funkcia mení zakrivenie. Funkcia je preto rýdzo konkávna na intervale, kde . Analogicky sa odvodí pravidlo pre interval konkávnej funkcie . Daná derivácia musí existovať. To, že funkcia je diferencovateľná nevyplýva priamo z podmienky spojitosti skúmanej funkcie, preto treba pridať podmienku diferencovateľnosti.






