Herónov vzorec je vzorec na výpočet obsahu všeobecného trojuholníka (v euklidovskej rovine), pomocou dĺžok jeho strán.
Ak sú  dĺžky strán trojuholníka, platí pre jeho obsah
dĺžky strán trojuholníka, platí pre jeho obsah
 ,
kde
,
kde  je polovičný obvod trojuholníka.
je polovičný obvod trojuholníka.
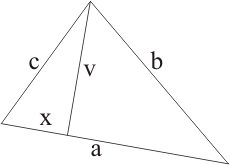
Označme  vzdialenosť vrcholu
vzdialenosť vrcholu  od päty kolmice z vrcholu
od päty kolmice z vrcholu  na stranu
na stranu  (výška). Pre ostrouhlý trojuholník na obrázku platí:
(výška). Pre ostrouhlý trojuholník na obrázku platí:


Odčítame od druhej rovnice prvú, dostaneme:

Z tohto vzťahu vyjadríme  :
:

Toto platí aj v pravouhlom trojuholníku, v tupouhlom sa namiesto  dáva
dáva  (viď. nižšie). Ak do prvej rovnice dosadíme
(viď. nižšie). Ak do prvej rovnice dosadíme  , získame výšku
, získame výšku  :
:





Ak dosadíme túto výšku do vzorca pre obsah trojuholníka  , dostaneme:
, dostaneme:

Ďalej pomocou rozkladov upravíme výraz pod odmocninou:

![{\displaystyle S={\frac {\sqrt {\left[\left(a+c\right)^{2}-b^{2}\right]\left[b^{2}-\left(a-c\right)^{2}\right]}}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969166500f7081e194f0dd52dfd83a1e3bcd549f)

Dosadíme polovičný obvod  ,
,  a dostávame výsledný vzorec:
a dostávame výsledný vzorec:



Vzorec bol formulovaný Herónom z Alexandrie a dôkaz bol publikovaný v jeho knihe Métrika, napísanej v roku 60 pred Kr.[1]
- Kratší dôkaz je možný pomocou kosínusovej vety.
- Obsah trojuholníka je symetrická kvadraticky homogénna funkcia jeho strán.
Tento článok je čiastočný alebo úplný preklad článku Heronův vzorec na českej Wikipédii.
























![{\displaystyle S={\frac {\sqrt {\left[\left(a+c\right)^{2}-b^{2}\right]\left[b^{2}-\left(a-c\right)^{2}\right]}}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969166500f7081e194f0dd52dfd83a1e3bcd549f)





