Perturbácia (astronómia)
Perturbácia (odchýlka) v astronómii je komplexný pohyb masívneho telesa ovplyvnený inými silami ako je gravitačná príťažlivosť iného jedného masívneho telesa.[1] Iné sily môžu zahŕňať tretie (štvrté, piate atď.) teleso, odpor napr. atmosféry a mimo-stredovú príťažlivosť sféroidu alebo inak nepravidelného telesa.

Úvod[upraviť | upraviť zdroj]
Štúdium perturbácii začalo s prvými pokusmi predpovedať pohyby planét na oblohe, aj keď v staroveku príčiny zostávali mýtické. Keď Newton formuloval pohybové zákony a zákon všeobecnej gravitácie, aplikoval ich na prvú analýzu perturbácii, spoznal komplexnú zložitosť ich výpočtu. [2] Mnoho iných veľkých matematikov odvtedy venovalo pozornosť súvisiacim problémom. V 18. a 19. storočí navigácia na mori vyžadovala presné tabuľky pozícii Mesiaca a planét .
Komplexné pohyby gravitačných perturbací možno rozdeliť. Hypotetický pohyb daného telesa pod gravitačným vplyvom iba iného telesa je zvyčajne kužeľosečka a možno ju ľahko opísať metódami geometrie. Nazýva sa to problém dvoch telies. Rozdiely medzi týmto a skutočným pohybom telesá sú perturbácie spôsobené dodatočnými gravitačnými účinkami ďalšieho telesa alebo telies. Ak existuje iba jedno ďalšie dôležité teleso, potom je perturbačný (odchýlený) pohyb problém troch telies . Ak existuje viac iných telies, je to problém n telies. Analytické riešenia (matematické výrazy na predikciu pozícii a pohybov v akomkoľvek budúcom čase) pre problém dvoch a troch telies existuje, ale zatiaľ nie sú známe pre problém n telies okrem niektorých špeciálnych prípadov. Dokonca aj problém dvoch telies sa stane neriešiteľným, ak má jedno z telies nepravidelný tvar. [3]
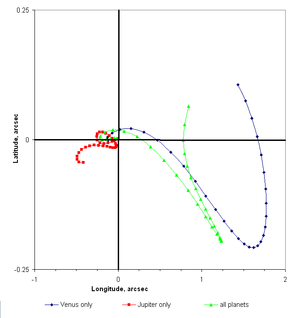
Väčšina systémov obsahujúcich viacnásobné gravitačné príťažlivosti prezentuje jedno primárne teleso, ktoré je dominantné vo svojich vplyvoch (napr. hviezda v prípade hviezdy a jej planéty, alebo planéta v prípade planéty a jej satelitu). Gravitačné vplyvy iných telies možno uvažovať ako perturbácie hypotetického nevychýleného pohybu planéty alebo satelitu okolo jeho primárneho telesa.
Matematická analýza[upraviť | upraviť zdroj]
Všeobecné perturbácie[upraviť | upraviť zdroj]
V metódach všeobecných perturbácii sa diferenciálne rovnice, buď pohybu alebo zmeny orbitálnych elementov, rieši analyticky zvyčajne použitím rozvojov radov. Výsledok je zvyčajne vyjadrený pomocou algebraických a trigonometrických funkcií dráhových elementov daného telesa a perturbujúcích telies. Tento postup možno všeobecne aplikovať na mnoho rôznych podmienok a nie je špecifický pre nejakú určitú zostavu gravitačných objektov.
Periodická povaha[upraviť | upraviť zdroj]

V slnečnej sústave je veľa rušení jednej planéty druhou periodických, zložených z malých impulzov vznikajúcich zakaždým, keď sa planéty priblížia na svojich orbitách. To spôsobuje, že telesá konajú pohyby, ktoré sú periodické alebo kvaziperiodické, napr. Mesiac na svojej silne odchýlenej dráhe, ktorá je predmetom lunárnej teórie. Táto periodicita viedla k objavu Neptúna v roku 1846 ako výsledok jeho perturbácii na dráhu Uránu.
Referencie[upraviť | upraviť zdroj]
- ↑ BATE, Roger R.; MUELLER, Donald D.; WHITE, Jerry E.. Fundamentals of Astrodynamics. [s.l.] : Dover Publications, Inc., New York, 1971. ISBN 0-486-60061-0. , e.g. at ch. 9, p. 385.
- ↑ Newton in 1684 wrote: "By reason of the deviation of the Sun from the center of gravity, the centripetal force does not always tend to that immobile center, and hence the planets neither move exactly in ellipses nor revolve twice in the same orbit. Each time a planet revolves it traces a fresh orbit, as in the motion of the Moon, and each orbit depends on the combined motions of all the planets, not to mention the action of all these on each other. But to consider simultaneously all these causes of motion and to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind." (quoted by Prof G E Smith (Tufts University), in "Three Lectures on the Role of Theory in Science" 1. Closing the loop: Testing Newtonian Gravity, Then and Now); and Prof R F Egerton (Portland State University, Oregon) after quoting the same passage from Newton concluded: "Here, Newton identifies the "many body problem" which remains unsolved analytically." Archivované 2005-03-10 na Wayback Machine
- ↑ ROY, A.E.. Orbital Motion. third. vyd. [s.l.] : Institute of Physics Publishing, 1988. ISBN 0-85274-229-0. , chapters 6 and 7.
- ↑ Gravity Simulator [online]. www.orbitsimulator.com, [cit. 2019-11-18]. Dostupné online.
Pozri aj[upraviť | upraviť zdroj]
Zdroj[upraviť | upraviť zdroj]
- Tento článok je čiastočný alebo úplný preklad článku Perturbation (astronomy) na anglickej Wikipédii.
