Komplexné číslo
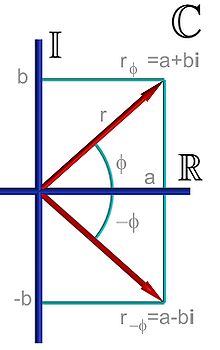
Komplexné čísla sú zovšeobecnením pojmu reálneho čísla. V obore reálnych čísel nemajú všetky polynomiálne rovnice riešenie. Ak sa číslo i definuje ako riešenie rovnice , potom všetky polynomiálne (algebrické) rovnice riešenie mať budú.
Reálne čísla[upraviť | upraviť zdroj]
Reálne čísla sa nachádzajú v jednom rade usporiadané podľa veľkosti. Tento rad reálnych čísel sa nazýva číselná os. Číselná os má rozmedzie od mínus nekonečna až po plus nekonečno. Túto os je možné predstaviť si ako priamku, ktorá leží v rovine. Logicky tak vznikne možnosť, že aj v iných bodoch roviny okrem bodov tejto priamky je možné nájsť nejaké čísla.
Imaginárne čísla[upraviť | upraviť zdroj]
V iných miestach roviny sa nachádzajú čísla, ktoré nazývame imaginárne čísla. Spolu so všetkými reálnymi číslami tvoria množinu všetkých komplexných čísel. Definoval ich nemecký matematik Gauss a podľa neho sa aj táto rovina čísel pomenovala Gaussova rovina. Túto rovinu rozdeľujú dve osi — už spomínaná číselná os, ktorá sa v grafoch stotožňuje s osou x (reálna os), a na ňu kolmú os y (imaginárna os). Obe tieto osi sa pretínajú v bode [0;0].
Zápis komplexných čísel[upraviť | upraviť zdroj]
Komplexné čísla sa od reálnych líšia svojím zápisom. Kým na zápis reálneho čísla potrebujeme iba jedno reálne číslo, ktoré určuje jeho polohu na číselnej osi, na zápis komplexného čísla potrebujeme dve reálne čísla. Jedno určuje reálnu časť komplexného čísla — jeho priemet do osi x — a druhé jeho imaginárnu časť — jeho priemet do osi y. Komplexné číslo potom zapíšeme ako výraz a + b*i, kde a je jeho reálna časť, b je jeho imaginárna časť a i je jednotkový vektor v Gaussovej rovine v smere imaginárnej osi y. Podobne je číslo 1 jednotkovým vektorom v smere osi x. Na osi x je napríklad číslo 8 dané ako 8-násobok jednotkového vektora 1, t. j. 8 = 8*1. Tento jednotkový vektor však kvôli úspornosti nepíšeme. V druhom člene výrazu však musíme použiť písmeno i, keďže nejde o reálne číslo. Čiže zápis čísla uvedeného na obrázku bude: 3 + 4*i.
Algebrický tvar[upraviť | upraviť zdroj]
Zápis komplexných čísel v tvare a + bi, kde a, b sú reálne čísla sa nazýva algebrický tvar komplexných čísel. Z obrázku vidieť, že každé komplexné číslo v rovine možno zaznačiť ako vektor so začiatkom v bode so súradnicami [0;0] a koncom v súradniciach daných zápisom tohto čísla, v tomto prípade [3;4].
Dve komplexné čísla sú rovnaké práve vtedy, ak vektory, ktoré ich predstavujú, sú rovnaké.
Goniometrický tvar[upraviť | upraviť zdroj]
Existujú aj ďalšie spôsoby, ktorými môžeme zapísať komplexné číslo. Jedným z nich je goniometrický tvar komplexného čísla. Pri tomto zápise je potrebné poznať dve veci:
- veľkosť komplexného čísla, t. j. veľkosť vektora, ktorým je znázornené v Gaussovej rovine
- uhol ktorý zviera s reálnou osou x.
Potom má komplexné číslo tvar
kde |z| je veľkosť komplexného čísla a je uhol, ktorý zviera s reálnou osou. Tento tvar je veľmi jednoducho možné odvodiť z pravouhlého trojuholníka, ktorý vznikne priemetmi vektora komplexného čísla na reálnu a imaginárnu os a zo znalostí funkcií sínus a kosínus.
Použitie[upraviť | upraviť zdroj]
Využívajú sa vo fyzike, elektronike alebo v 3D grafike.
Vo fyzike sa využívajú tam, kde sa pracuje s vlnami, napr. elektromagnetické polia (Maxwellove rovnice), vlnové funkcie elektrónov, v aerodynamike alebo hydrodynamike.
Keď sa napr. v elektrotechnike pracuje so striedavými prúdmi a v obvode sú okrem odporov aj kondenzátory alebo cievky. Vtedy sa pri využití komplexných čísel počíta tak, akoby boli v obvode len odpory, čo výpočet zjednodušuje. Keby sa ten istý obvod počítal bez komplexných čísel, celý postup by sa skomplikoval.
V 3D grafike sa komplexné čísla používajú, keď sa počítajú aj lomy svetla na rozhraní priesvitných materiálov alebo na tenkých vrstvách (olej na vode). Takto sa vytvárajú aj bez rádiozity vysoko reálne obrázky.
Operácie s komplexnými číslami[upraviť | upraviť zdroj]
S komplexnými číslami je možné vykonávať také isté operácie ako s reálnymi číslami, t. j. sčítavanie, odčítavanie, násobenie, delenie, umocňovanie alebo odmocňovanie. Všetky tieto operácie sú analogické operáciám s reálnymi číslami.
Hlavné funkcie[upraviť | upraviť zdroj]
Majme komplexné číslo z = a + bi, potom:
reálna časť -
imaginárna časť -
uhol zvierajúci s reálnou osou (argument) - (pre naše operácie v radiánoch)
absolútna hodnota - veľkosť komplexného čísla -
Sčítavanie komplexných čísel[upraviť | upraviť zdroj]

Dve komplexné čísla sa sčítavajú tak, že sa sčítajú ich vektory. Do koncového bodu vektora prvého čísla sa umiestni začiatočný bod vektor/vektora druhého čísla. Výsledkom je vektor, ktorý spája začiatočný bod vektora prvého čísla s koncovým bodom vektora druhého čísla. Výsledkom sú koncové súradnice výsledného vektora v Gaussovej rovine. Súčet dvoch komplexných čísel možno urobiť aj algebricky: Majme dve komplexné čísla, (a + b*i) a (c + d*i). Ich súčet vypočítame ako (a + b*i) + (c + d*i) = a + c + b*i + d*i = [(a +c) + i*(b + d)]. Vidno, že súčtom dvoch komplexných čísel je znovu komplexné číslo, ktorého reálna časť je (a + c) a imaginárna časť je (b + d).
Ak máme dané dve komplexné čísla a , tak ich súčet je komplexné číslo, pre ktoré platí:
Ak chceme sčítať viac komplexných čísel, najprv sčítame podľa vyššie uvedeného spôsobu dve čísla, potom k výslednému vektoru pripočítame vektor tretieho čísla atď.
Odčítavanie komplexných čísel[upraviť | upraviť zdroj]
Postupujeme tým istým spôsobom ako pri sčítavaní. Do koncového bodu vektora prvého čísla umiestnime začiatočný bod vektora druhého čísla, ale tento vektor bude otočený o 180° oproti pôvodnému vektoru druhého čísla. Výsledným vektorom je opäť spojnica začiatočného bodu vektora prvého čísla a koncového bodu vektora druhého čísla.
Rozdiel dvoch komplexných čísel možno urobiť aj algebricky: Majme dve komplexné čísla, (a + b*i) a (c + d*i). Ich rozdiel vypočítame ako (a + b*i) – (c + d*i) = a – c + b*i – d*i = [(a – c) + i*(b – d)]. Vidíme, že rozdielom dvoch komplexných čísel je znovu komplexné číslo, ktorého reálna časť je (a – c) a imaginárna časť je (b – d).
Ak máme dané dve komplexné čísla x = a + b*i a y = c + d*i, tak ich rozdiel je komplexné číslo, pre ktoré platí:
Pri odčítavaní viacerých komplexných čísel odčítame najprv od vektora prvého čísla vektor druhého čísla, od výsledného vektora vektor tretieho čísla atď.
Násobenie komplexných čísel[upraviť | upraviť zdroj]

Násobenie komplexných čísel zahŕňa v sebe dve geometrické transformácie, rovnoľahlosť (t. j. natiahnutie alebo skrátenie) a otáčanie.
Keď v Gaussovej rovine násobíme dvomi reálne číslo 3, dostaneme reálne číslo 6. Jeho vektor je v Gaussovej rovine dvojnásobne natiahnutý oproti vektoru pôvodného čísla 3. Čiže násobenie reálnych čísel môžeme geometricky chápať ako naťahovanie (prípadne skracovanie) vektora pôvodného čísla.
Pri násobení komplexných čísel nevystačíme len s jednou geometrickou transformáciou v rovine. Na pomoc si vezmeme ešte otáčanie. Ak chceme vynásobiť dve komplexné čísla, musíme najprv otočiť proti smeru pohybu hodinových ručičiek prvé číslo o uhol, ktorý zviera druhé číslo s reálnou osou a potom ho ešte musíme natiahnuť na toľko násobok jeho dĺžky, aká je absolútna hodnota druhého čísla. Inak povedané: Pri násobení dvoch komplexných čísel musíme vypočítať súčet uhlov, ktoré zvierajú vektory daných komplexných čísel s reálnou osou x. Výsledný vektor bude s osou x zvierať uhol rovný súčtu pôvodných uhlov vektorov daných čísel. Veľkosť výsledného vektora bude predstavovať súčin absolútnych hodnôt veľkostí vektorov daných čísel.
Násobiť viac komplexných čísel znamená vynásobiť najprv dve a potom výsledný vektor vynásobiť tretím komplexným číslom atď.
Podobne ako súčet a rozdiel, nemusíme súčin dvoch komplexných čísel robiť iba graficky. Môžeme ho vyjadriť aj výpočtom. Nech sú dané dve komplexné čísla x = a + bi, y = c + di, ich súčin je:
V poslednom zápise sa vyskytuje číslo i umocnené na druhú. Čomu sa rovná tento výraz? Skúsme už s našimi vedomosťami vynásobiť číslo i samo sebou. Vieme, že toto číslo je jednotkový vektor na imaginárnej osi y, čiže zviera s osou x uhol veľkosti 90°. Keď násobíme dané číslo samo sebou, potom súčet uhlov musí byť dvakrát väčší ako pôvodný uhol. Čiže výsledný vektor bude ležať v smere 180° od osi x. Z toho vyplýva, že výsledný vektor bude ležať na osi x, ale v jej zápornej časti. Veľkosť tohto vektora bude 1*1 = 1, pretože vektor i má veľkosť 1 (jednotkový vektor). Tým zisťujeme, že vektor čísla i² bude ležať na reálnej osi x, bude mať veľkosť 1 a bude orientovaný v jej zápornom smere. Výsledné číslo tým bude mať súradnice [–1;0]. Čiže môžeme napísať slávny vzťah:
Po vyjadrení i² = –1 dostávame pre súčin dvoch komplexných čísel vzťah:
V tejto poslednej rovnici je výraz (a*c – b*d) reálnou časťou komplexného čísla (súradnica na osi x) a výraz (a*d + b*c)i je imaginárnou časťou komplexného čísla (výraz v zátvorke určuje súradnicu a písmeno i pred zátvorkou naznačuje, že ide o súradnicu osi y). Perfektné je to, že sme zistili, že súčinom dvoch komplexných čísel je znovu komplexné číslo! Naša definícia násobenia je teda v poriadku.
Ak máme dané dve komplexné čísla x = a + bi a y = c + di, tak ich súčin je komplexné číslo, pre ktoré platí:
Delenie komplexných čísel[upraviť | upraviť zdroj]
Čitateľa aj menovateľa zlomku vynásobíme výrazom (c - di). Menovateľ sa potom dá upraviť do tvaru c² + d², a teda môžeme deliť reálnym číslom.
Exponenciálna funkcia[upraviť | upraviť zdroj]
Máme umocniť ea + bi. Ak použijeme vetu o násobení mocnín s rovnakým základom v opačnom smere, dostaneme eaebi. Funkciu ea vieme umocniť, keďže a je reálne číslo. Lenže čomu sa rovná výraz ebi? Z Taylor-Maclaurinovho radu poznáme vzorec pre exponenciálnu funkciu:
Ak do tohto vzorca za x dosadíme xi, dostaneme:
alebo po inom usporiadaní
V zátvorkách je znova podľa Taylor-Maclaurinovho radu cos x, resp. sin x. Z toho
Pre komplexné číslo z = a + bi:
Prirodzený logaritmus[upraviť | upraviť zdroj]
Na vyjadrenie prirodzeného logaritmu použijeme vzorec
z toho vyplýva (rovnica 1)
Vieme, že (cos x + i sin x) je komplexná jednotka, tj. komplexné číslo, ktorého absolútna hodnota je 1. Ak chápeme x ako argument nejakého komplexného čísla z a celý výraz vynásobíme absolútnou hodnotou tohto čísla, dostaneme goniometrické vyjadrenie komplexného čísla. Vieme, že
- .
Toto použijeme v rovnici 1, kde x zameníme za Abs(z) = |z| a y za (cos x + i sin x). Dostaneme
Pre komplexné číslo z = a + bi:
Umocňovanie komplexných čísel[upraviť | upraviť zdroj]
Z predchádzajúcich častí vieme, že ak chceme umocniť komplexné číslo reálnym, umocníme jeho veľkosť (absolútnu hodnotu) a vynásobíme jeho argument daným reálnym číslom:
kde je argument daného komplexného čísla.
Ak chceme umocniť komplexné číslo komplexným číslom, vychádzame zo vzorca
- ,
pretože už máme určenú exponenciálnu aj logaritmickú funkciu. Majme dané dve komplexné čísla
Potom
Označme
Ku predchádzajúcej rovnosti píšeme ďalej
Potom pre výsledok
píšeme
Trigonometrické funkcie[upraviť | upraviť zdroj]
Majme dané komplexné číslo z = a + bi, potom:
Cyklometrické funkcie[upraviť | upraviť zdroj]
Majme dané komplexné číslo z = a + bi, potom:




























![{\displaystyle \ln {\Big [}|z|(\cos x+\mathbf {i} \sin x){\Big ]}=\ln |z|+\mathbf {i} \operatorname {Arg} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b6bbf5b34a5528c309ae5bc7e9cd7a5ec0e70ca)






![{\displaystyle {\begin{aligned}z_{1}^{z_{2}}&=\exp(z_{2}\ln z_{1})=\\&=\exp {\bigg \{}{\Big [}a_{2}+b_{2}\mathbf {i} {\Big ]}{\Big [}\ln |z_{1}|+\mathbf {i} \operatorname {Arg} (z_{1}){\Big ]}{\bigg \}}=\\&=\exp {\bigg \{}{\Big [}a_{2}\ln |z_{1}|-b_{2}\operatorname {Arg} (z_{1}){\Big ]}+\mathbf {i} {\Big [}a_{2}\operatorname {Arg} (z_{1})+b_{2}\ln |z_{1}|{\Big ]}{\bigg \}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9a2324593d28409ea93aa184fdcb02f113e9da6)












![{\displaystyle \arctan z={\frac {\mathbf {i} \left[\ln(1-\mathbf {i} z)-\ln(1+\mathbf {i} z)\right]}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab686dcd90810735e569e182597d4231a907ccbf)
![{\displaystyle \operatorname {arccot} z={\frac {\mathbf {i} }{2}}\left[\ln \left({\frac {z-\mathbf {i} }{z}}\right)-\ln \left({\frac {z+\mathbf {i} }{z}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/377cfa5f0de9660766cc511351e8e8a3e3b033bf)

