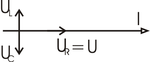Rezonančný obvod
Rezonančný obvod alebo RLC obvod, LC obvod je komplexný jednobran. Vznikne paralelným alebo sériovým spojením kondenzátora a cievky. Pri jednej, tzv. rezonančnej frekvencii sa v tomto obvode vyrovnáva kapacitná a induktívna reaktancia a rezonančný obvod sa pri tejto frekvencii chová ako činný odpor. Stav obvodu, ktorý nastane pri rezonančnej frekvencii, sa nazýva rezonancia. Prúd pretekajúci obvodom je v tomto stave maximálny a odpor minimálny.
Keď sú cievka a kondenzátor spolu zapojené, elektrický prúd medzi nimi kmitá pri frekvencii
kde L je indukčnosť cievky vyjadrená v jednotkách henry a C je elektrická kapacita kondenzátora vyjadrená vo faradoch.
Vzťahy pre rezonančnú frekvenciu[upraviť | upraviť zdroj]
Pri rezonancii sa reaktancie rovnajú
Sériový rezonančný obvod[upraviť | upraviť zdroj]
Sériový rezonančný obvod má pri rezonančnej frekvencii najmenšiu impedanciu a najväčší prúd, pričom tento je v obvode konštantný.

Sériový rezonančný obvod sa využíva tam kde potrebujeme dosiahnuť maximálny prúd. Pri rezonančnej frekvencii sa indukčná reaktancia (induktancia) XL rovná kapacitnej reaktancii XC. Po dosadení môžeme odvodiť Thomsonov vzorec, ktorý je fO rezonančné = < [Hz]
- Pri frekvenci nižšej, ako je rezonančná:
- Pri rovnakej frekvencii ako je rezonančná:
- Pri frekvencii vyššej ako je rezonančná
Vzorce[upraviť | upraviť zdroj]
Činiteľ akosti[upraviť | upraviť zdroj]
V komponentoch skutočného rezonančného obvodu vznikajú pri prechode prúdu straty. Skutočnú cievku môžeme nahradiť ideálnou bezstratovou cievkou a stratovým odporom. Skutočný kondenzátor môžeme nahradiť ideálnym kondenzátorom a stratovým odporom - RSO = RL + RC. Činiteľ akosti sa označuje Q.
![]()
![]()
- Činiteľ akosti v obvode naprázdno
Udáva koľkokrát je väčšie napätie na cievke (kondenzátore) pri rezonančnej frekvencii ako napätie na odpore, a ako je celkové napätie.
Paralelný rezonančný obvod[upraviť | upraviť zdroj]
Využíva sa napríklad v oscilátoroch ako riadiaci člen. Po dodaní prúdového impulzu nastávajú tlmené prúdové kmity. Paralelný rezonančný obvod sa využíva i v elektromotoroch na kompenzáciu strát.