Rungeho jav

Červená krivka znázorňuje Rungeho funkciu.
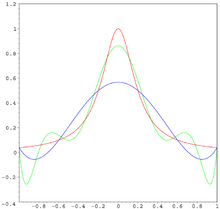
Modrá krivka je interpolačný polynóm piateho stupňa (s použitím šiestich ekvidištančných uzlov).
Zelená krivka znázorňuje interpolačný polynóm deviateho stupňa (s použitím desiatich ekvidištančných uzlov).
V interpolačných bodoch je chyba (z definície interpolácie) nulová. Medzi interpolačnými uzlami (zvlášť okolo bodov -1 a 1) však chyba pre polynómy vyššieho stupňa neúmerne narastá.

Rungeho jav je v numerickej matematike názov pre problém, ktorý vzniká pri interpolácii polynómom vyššieho stupňa. Je pomenovaný po Carlovi Davidovi Tolméovi Rungeovi, ktorý ho objavil, keď skúmal chybu polynomiálnej interpolácie istej triedy funkcií, dnes známych ako Rungeho funkcie. Tento jav je podobný Gibbsovmu javu pri Fourierových radoch.

Problém

Uvažujme funkciu:

$f(x)={\frac {1}{1+25x^{2}}}.\,$

Runge objavil, že pokiaľ sa táto funkcia (nazývaná aj Rungeho funkcia) interpoluje na intervale $<-1;1>$ pomocou ekvidištančných uzlov $x_{i}$, teda

$x_{i}=-1+(i-1){\frac {2}{n}},\quad i\in \left\{1,2,\dots ,n+1\right\},$

polynómom P_n(x) stupňa n, výsledná interpolačná krivka v okolí krajov intervalu (teda bodov −1 a 1) silne osciluje (čím narastá chyba interpolácie). Dá sa dokázať, že chyba interpolácie speje s rastúcim stupňom polynómu do nekonečna, teda platí:

$\lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=+\infty .$

Na druhej strane však Weierstrassova veta o aproximácii hovorí, že existuje postupnosť aproximujúcich polynómov, pre ktoré sa chyba limitne blíži k nule. Z toho vyplýva, že polynómy vysokého stupňa nemusia byť pri použití ekvidištančných uzlov optimálnym riešením.

Dôvod problému

Jeden zo základných poznatkov teórie interpolácie je, že chyba interpolačného polynómu rádu N je daná vzorcom

$f(x)-P_{N}(x)={\frac {f^{(N+1)}(\xi )}{(N+1)!}}\prod _{i=0}^{N}(x-x_{i})$

pre nejaké $\xi$ z intervalu (−1, 1).

Pre Rungeho funkciu

$f(x)={\frac {1}{1+25x^{2}}}$

majú prvé dve derivácie hodnoty:

${\begin{array}{lcl}\displaystyle f'(x)=-{\frac {50x}{\left(1+25x^{2}\right)^{2}}}&{\text{teda}}&\displaystyle \left|f'(1)\right|={\frac {50}{26^{2}}}\approx 0.0740;\\[1.5em]\displaystyle f''(x)={\frac {5000x^{2}-50(1+25x^{2})}{\left(1+25x^{2}\right)^{3}}}&{\text{teda}}&\displaystyle \left|f''(1)\right|={\frac {3700}{26^{3}}}\approx 0.2105.\end{array}}$

Absolútne hodnoty derivácií vyšších rádov môžu byť ešte väčšie. Z toho vyplýva, že sa zvyšuje aj horná hranica chyby interpolácie medzi interpolačnými uzlami.

Zmiernenie problému

Oscilácia interpolačného polynómu môže byť zmiernená, pokiaľ budú mať interpolačné uzly väčšiu hustotu v krajných častiach intervalu. Konkrétne, na intervale (−1,1) možno vybrať uzly s asymptotickou hustotou danou vzorcom $1/{\sqrt {1-x^{2}}}$. Štandardným príkladom množiny interpolačných uzlov spĺňajúcich túto vlastnosť sú tzv. Čebyšovove uzly, pre ktoré je zaručené, že maximálna chyba sa s rastúcim stupňom polynómu zmenšuje. Rungeho jav je teda dôkazom, že ekvidištančné uzly sú pre polynómy vyššieho stupňa nevhodné. Problém ale môže byť odstránený použitím splajnových kriviek, teda kriviek, ktoré sú po častiach polynomiálne. Pri splajnových krivkách sa dá chyba zmenšiť jednoducho zväčšením počtu deliacich bodov, a teda nie je potrebné zvyšovať stupeň polynómu.

Ďalšou použiteľnou metódou je interpolácia polynómom nižšieho rádu pomocou metódy najmenších štvorcov. Vo všeobecnosti, pri použití m ekvidištančných uzlov pre interpoláciu polynómom stupňa N, ak $N<2{\sqrt {m}}$, tak výsledný interpolačný polynóm $P_{N}(x)$ má dobré vlastnosti.

Pozri aj

• Gibbsov jav
• Taylorov polynóm
• Čebyšovov uzol

Zdroj

Tento článok je čiastočný alebo úplný preklad článku Runge's phenomenon na anglickej Wikipédii.