Kvadrika alebo kvadratická plocha je plocha 2. stupňa v trojrozmernom priestore . Teda ide o plochy , ktoré v pravouhlej súradnicovej sústave
{
0
,
x
,
y
,
z
}
{\displaystyle \{0,x,y,z\}}
a
x
2
+
b
y
2
+
c
z
2
+
d
x
y
+
e
z
y
+
f
x
z
+
g
x
+
h
y
+
i
z
+
j
=
0
{\displaystyle ax^{2}+by^{2}+cz^{2}+dxy+ezy+fxz+gx+hy+iz+j=0}
V priestore majme danú rovinu
k
{\displaystyle k}
kužeľosečku
K
{\displaystyle K}
V
{\displaystyle V}
Množina bodov všetkých priamok
V
,
X
{\displaystyle V,X}
X
∈
K
{\displaystyle X\in K}
V
=
[
0
,
0
,
0
]
{\displaystyle V=[0,0,0]}
K
:
z
=
c
{\displaystyle K:z=c}
c
≠
0
{\displaystyle c\neq 0}
(
x
−
m
n
z
)
2
a
2
+
(
y
−
n
n
z
)
2
b
2
−
z
2
c
2
=
0
{\displaystyle {\frac {(x-{\frac {m}{n}}z)^{2}}{a^{2}}}+{\frac {(y-{\frac {n}{n}}z)^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0}
(
x
−
m
n
z
)
2
a
2
−
(
y
−
n
n
z
)
2
b
2
−
z
2
c
2
=
0
{\displaystyle {\frac {(x-{\frac {m}{n}}z)^{2}}{a^{2}}}-{\frac {(y-{\frac {n}{n}}z)^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0}
c
(
y
−
n
c
z
)
2
−
2
p
(
x
−
m
c
z
)
z
=
0
{\displaystyle c(y-{\frac {n}{c}}z)^{2}-2p(x-{\frac {m}{c}}z)z=0}
V priestore majme danú rovinu
k
{\displaystyle k}
K
{\displaystyle K}
p
{\displaystyle p}
k
{\displaystyle k}
p
{\displaystyle p}
K
{\displaystyle K}
p
≡
P
;
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle p\equiv {P;{\vec {v}}=(v_{1},v_{2},v_{3})}}
(
x
−
v
1
v
3
z
)
2
a
2
+
(
y
−
v
2
v
3
z
)
2
b
2
=
1
{\displaystyle {\frac {(x-{\frac {v_{1}}{v_{3}}}z)^{2}}{a^{2}}}+{\frac {(y-{\frac {v_{2}}{v_{3}}}z)^{2}}{b^{2}}}=1}
(
x
−
v
1
v
3
z
)
2
a
2
−
(
y
−
v
2
v
3
z
)
2
b
2
=
1
{\displaystyle {\frac {(x-{\frac {v_{1}}{v_{3}}}z)^{2}}{a^{2}}}-{\frac {(y-{\frac {v_{2}}{v_{3}}}z)^{2}}{b^{2}}}=1}
(
y
−
v
2
v
3
z
)
2
−
2
p
(
x
−
v
1
v
3
z
)
=
0
{\displaystyle (y-{\frac {v_{2}}{v_{3}}}z)^{2}-2p(x-{\frac {v_{1}}{v_{3}}}z)=0}
Bližšie informácie v hlavnom článku: Elipsoid Elipsoid Elipsoid je stredová kvadrika s tromi rovinami súmernosti, ktoré pretínajú plochu v elipsách. Kanonické rovnice elipsoidu sú
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}
a
=
b
{\displaystyle a=b}
a
=
b
=
c
{\displaystyle a=b=c}
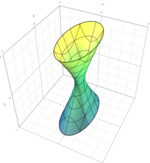
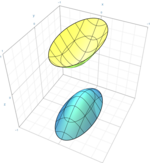
Jednodielny hyperboloid Dvojdielny hyperboloid Kanonické rovnice hyperboloidu sú
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1}
−
x
2
a
2
−
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle -{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}
Jednodielny resp. dvojdielny hyperboloid sú stredové kvadriky s tromi rovinami súmernosti, pričom roviny
x
=
0
{\displaystyle x=0}
y
=
0
{\displaystyle y=0}
z
=
0
{\displaystyle z=0}
elipse resp. nemá s plochou žiaden spoločný bod. Hyperboloidy, pre ktoré platí
a
=
b
{\displaystyle a=b}
Hyperbolický paraboloid Paraboloid je nestredová kvadrika s dvomi rovinami súmernosti, ktoré pretínajú plochu v parabolách. Kanonické rovnice paraboloidu sú
x
2
p
+
y
2
q
=
2
z
{\displaystyle {\frac {x^{2}}{p}}+{\frac {y^{2}}{q}}=2z}
x
2
p
−
y
2
q
=
2
z
{\displaystyle {\frac {x^{2}}{p}}-{\frac {y^{2}}{q}}=2z}
kde
p
,
q
{\displaystyle p,q}
a
(
x
−
s
1
)
2
+
b
(
y
−
s
2
)
2
+
c
(
z
−
s
3
)
2
+
d
=
0
{\displaystyle a(x-s_{1})^{2}+b(y-s_{2})^{2}+c(z-s_{3})^{2}+d=0}
M
=
[
m
1
,
m
2
,
m
3
]
{\displaystyle M=[m_{1},m_{2},m_{3}]}
a
(
m
1
−
s
1
)
(
x
−
s
1
)
+
b
(
m
2
−
s
2
)
(
y
−
s
2
)
+
c
(
m
3
−
s
3
)
(
z
−
s
3
)
+
d
=
0
{\displaystyle a(m_{1}-s_{1})(x-s_{1})+b(m_{2}-s_{2})(y-s_{2})+c(m_{3}-s_{3})(z-s_{3})+d=0}
Dotyková rovina kvadrickej plochy
a
(
x
−
s
1
)
2
+
b
(
y
−
s
2
)
2
−
c
(
z
−
s
3
)
2
=
0
{\displaystyle a(x-s_{1})^{2}+b(y-s_{2})^{2}-c(z-s_{3})^{2}=0}
M
=
[
m
1
,
m
2
,
m
3
]
{\displaystyle M=[m_{1},m_{2},m_{3}]}
a
(
m
1
−
s
1
)
(
x
−
s
1
)
+
b
(
m
2
−
s
2
)
(
y
−
s
2
)
+
c
(
z
+
m
3
−
2
s
3
)
=
0
{\displaystyle a(m_{1}-s_{1})(x-s_{1})+b(m_{2}-s_{2})(y-s_{2})+c(z+m_{3}-{2_{s}}_{3})=0}
M. Billich - M. Trenkler: Zbierka úloh z geometrie . Ružomberok, Verbum. 2013, s. 65 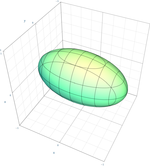









![{\displaystyle V=[0,0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0173f1bc2becc1edd8b65ecc0b20398110db3fa2)






















![{\displaystyle M=[m_{1},m_{2},m_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261682b1bcac79db542e1b187b6a84ec9688d998)


