Pohyb po kružnici

Pohyb po kružnici (iné názvy: kruhový pohyb (hmotného bodu), otáčavý (resp. rotačný) pohyb hmotného bodu) je taký pohyb, pri ktorom sa teleso pohybuje po kružnici, jeho trajektória je teda kruhová. Patrí medzi tzv. krivočiare pohyby. Tento pohyb môže byť rovnomerný, rovnomerne zrýchlený alebo nerovnomerne zrýchlený.

Príkladmi pohybu po kružnici sú točenie ventilátora; točenie guličky na konci pevného lana; pohyb pasažierov na retiazkového kolotoči, keď sa nemení vzdialenosť sedačiek od osi otáčania; obeh satelitu okolo planéty v konštantnej vzdialenosti od planéty; pohyb nabitých častíc, ak ich rýchlosť je kolmá na magnetické pole, v ktorom sa nachádzajú. Ak sa teleso otáča okolo pevnej osi, všetky body telesa vykonávajú pohyb po kružnici.

Opis pohybu po kružnici má širší význam než sa z jeho definície na prvý pohľad môže zdať, pretože (takmer) ľubovoľný krivočiary pohyb sa dá opísať tak, že ku krivke pohybu (teda trajektórii) v danom bode priložíme kružnicu, ktorá túto krivku v danom “záhybe” krivky čo najlepšie aproximuje (tzv. oskulačná kružnica) a potom počítame pomocou údajov pre túto kružnicu (existujú však pochopiteľne aj iné metódy opisu krivočiareho pohybu). Okrem toho v kontexte pohybu nie jedného hmotného bodu, ale nejakého celého telesa (presnejšie tzv. dokonalého tuhého telesa, teda tvarovo nemennej sústavy hmotných bodov) tvorí pohyb po kružnici základ analýzy tzv. otáčavého pohybu telesa (napríklad pohyb listu vrtule). Pri otáčavom pohybe majú jednotlivé časti (hmotné body) toho istého rotujúceho telesa (napr. listu vrtule) pochopiteľne rozličné rýchlosti, pretože opisujú rozlične veľké kružnice za ten istý čas podľa toho, ako sú ďaleko od osi otáčania; zároveň však majú zhodné uhlové rýchlosti. Rovnomerný pohyb po kružnici pri pohľade v rovine kružnice vyzerá rovnako ako lineárny harmonický pohyb.

Skrátená verzia nasledujúceho textu je uvedená v článku rýchlosť (fyzikálna veličina).

Uhlové veličiny opisujúce otáčavý pohyb a ich vzťah k posuvným veličinám

V kontexte pohybu po kružnici rozlišujeme medzi (posuvnou/“normálnou”) obvodovou rýchlosťou $\mathbf {v}$, (posuvným/obvodovým/“normálnym”) zrýchlením $\mathbf {a}$ a (“normálnou”) dráhou (s) na jednej strane a uhlovou rýchlosťou $\mathbf {\omega }$, uhlovým zrýchlením $\mathbf {\alpha }$ a uhlovou dráhou $\varphi$ na strane druhej.

Uhlová dráha je uhol, o aký sa teleso pohlo okolo osi otáčania. Uvádza sa v radiánoch a v radiánoch pre prejdenú dráhu a uhlovú dráhu platí

$s=\varphi r$,

kde $r$ je polomer otáčania, teda vzdialenosť telesa od osi otáčania. Uhlová rýchlosť je okamžitá zmena uhlovej dráhy za čas. Ak je polomer otáčania konštantný (napríklad teleso sa otáča okolo pevnej osi), platí

$v=\omega r$

a aj

$a=\alpha r$.

Rovnomerný pohyb po kružnici

Figure 1: Rýchlosť v a zrýchlenie a pri rovnomernom pohybe po kružnici. Veľkosť rýchlosti je konštantná a v smere dotyčnice ku kružnici, po ktorej sa bod pohybuje; zrýchlenie má konštantnú veľkosť a smeruje k osi otáčania.

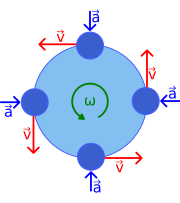
Toto je špeciálny prípad pohybu po kružnici, keď je uhlová rýchlosť otáčania konštantná a teda obvodová rýchlosť hmotného bodu nemení svoju veľkosť, iba svoj smer. Keďže vektor rýchlosti sa mení, hmotný bod má nenulové posuvné zrýchlenie, ktoré smeruje ku osi otáčania a nazýva sa dostredivé zrýchlenie. Vo vzťažnej sústave, ktorá vykonáva rovnomerný pohyb po kružnici, sa toto zrýchlenie prejavuje ako následok fiktívnej odstredivej sily.

Pre rovnomerný pohyb po kružnici platí

$\omega ={\frac {\Delta \varphi }{\Delta t}}={\frac {2\pi }{T}}=\ 2\pi f$,

kde $T$ je perióda pohybu a $f$ je frekvencia pohybu. Veľkosť dostredivého zrýchlenia je

$a={\frac {v^{2}}{r}}=\omega ^{2}r$.

Keďže uhlová rýchlosť je konštantná, uhlové zrýchlenie je nulové a prejdetá uhlová dráha $\varphi$ lineárne rastie v čase:

$\alpha =0$,

$\varphi =\omega t+\varphi _{0}$,

kde $\varphi _{0}$ je hodnota prejdenej uhlovej dráhy v čase $t=0$.

Obvodová rýchlosť je kolmá na smer sprievodič (čo je spojnica stredu kružnice, po ktorej sa pohyb uskutočňuje, s aktuálnou polohou hmotného bodu) a má pre všetky body v rovnakej vzdialenosti od osi otáčania rovnakú veľkosť.

Všeobecný prípad pohybu po kružnici

Pokiaľ ide o vzorce pohybu po kružnici, majme najprv dané toto:

• Základné vzorce platné pre akékoľvek výpočty rýchlosti a zrýchlenia (podrobnosti pozri v článku rýchlosť (fyzikálna veličina)):
  • t je čas
  • s (presnejšie s_b) je dĺžka oblúka (iné názvy: dĺžka/veľkosť dráhy, dráha, obvodová dráha a pod.)
  • r je polohový vektor
  • v_d = ds/dt je okamžitá dráhová rýchlosť
  • v = dr/dt =|v|.τ je vektor okamžitej rýchlosti
  • |v|= (+/-) v_d je veľkosť vektora okamžitej rýchlosti (pre pohyb v smere číslovania krivočiarej súradnice s |v|= v_d, pre pohyb v opačnom smere |v|= - v_d)
  • τ je jednotkový vektor v smere v a teda aj v smere a_t (tzv. tangenciálny jednotkový vektor) (čiže v=|v|. τ a a_t=|a_t|.τ); jeho konkrétny vzorec pri pohybe po kružnici je uvedený nižšie
  • a_d = dv_d/dt je okamžité dráhové zrýchlenie
  • a =dv/dt = a_t + a_n je vektor okamžitého zrýchlenia
  • |a_t| = d|v|/dt = (+/-) a_d je veľkosť vektora tangenciálneho (či dotyčnicového) zrýchlenia (pre zrýchlený pohyb |a_t|=a_d, pre spomalený pohyb |a_t|=- a_d)
  • |a_n|= |v|²/R je veľkosť vektora normálového zrýchlenia, ktoré najmä v kontexte pohybu po kružnici voláme aj dostredivé (či centripetálne) zrýchlenie (R je polomer oskulačnej kružnice; ak má nejaká dráha priamo tvar kružnice tak R sa rovná jednoducho polomeru kružnice)
  • |a| =$\textstyle {\sqrt {|{\boldsymbol {a}}_{t}|^{2}+|{\boldsymbol {a}}_{n}|^{2}}}$ je veľkosť vektora okamžitého zrýchlenia
  • a_t = |a_t|. τ je vektor tangenciálneho zrýchlenia
  • a_n = |v|.(dτ/dt) je vektor normálového zrýchlenia, ktoré sa najmä v kontexte pohybu po kružnici nazýva aj dostredivé (či centripetálne) zrýchlenie
  • ₀ znamená „na začiatku“ (t.j. v čase t₀)
• Ostatné:
  • stred kruhu je na zjednodušenie výkladu stotožnený s počiatkom karteziánskej súradnicovej sústavy
  • r je polomer kružnice (|r|=r)
  • T je perióda pohybu (iné názvy: obežná doba, perióda obehu, perióda otáčania, perióda a pod.), čo je doba jedného celého obehu po kružnici
  • f = 1/T je frekvencia (iné názvy: frekvencia otáčania, otáčky)
  • obvod kruhu = 2πr
  • ϕ je polohový uhol (iné názvy: uhlová súradnica, uhol otáčania), t.j. uhol medzi sledovaným polohovým vektorom a nejakým referenčným polohovým vektorom (ktorým je obyčajne x-ová os) meraný v smere y-ovej súradnice
  • ϕ je vektor polohového uhla; jeho smer je vždy kolmý na rovinu x-y (teda rovinu otáčania) a jeho veľkosť|ϕ| sa volá uhlová dráha (formálne je uhlová dráha síce len veľkosť kolmice na rovinu a nie priamo polohový uhol, platí však |ϕ|= ϕ)
  • ω = dϕ/dt =|ω| je (okamžitá) uhlová rýchlosť,
  • ω = dϕ/dt je vektor (okamžitej) uhlovej rýchlosti; jeho smer je vždy kolmý na rovinu x-y (teda rovinu otáčania), pričom jeho orientácia je zhodná s orientáciou vektora ϕ iba ak ϕ rastie, inak má opačnú orientáciu
  • α = dω/dt = d²ϕ/dt = |α| je (okamžité) uhlové zrýchlenie (alternatívne sa značí: ɛ); pozor na zámenu „α“ ako uhlového zrýchlenia s „α“ ako bežným označením uhlov (ide iba o náhodnú zhodu značenia)
  • α = dω/dt = d²ϕ/dt je vektor (okamžitého) uhlového zrýchlenia (alternatívne sa značí: ɛ); jeho smer je vždy kolmý na rovinu x-y (teda rovinu otáčania), pričom jeho orientácia je zhodná s orientáciou vektora ω iba ak ω rastie, inak má opačnú orientáciu
  • τ =(-sinϕ, cosϕ) – vysvetlenie pozri vyššie
  • τ_n =(-cosϕ, -sinϕ) je jednotkový vektor v smere a_n (tzv. normálový jednotkový vektor) a teda aj v smere opačnom než r (čiže a_n =|a_n|.τ_n a r=-|r|. τ_n = -r. τ_n)
  • τ_ω je jednotkový vektor v smere ω (čiže ω = |ω|. τ_ω= ω. τ_ω)
  • x (t.j. krížik) je znak vektorového súčinu…
• Δs = s-s₀; Δϕ = ϕ – ϕ₀; Δ|v|=|v| - |v₀|; Δt = t – t₀

Potom platí (popri vyššie uvedených vzorcoch):

• Δs = r.Δϕ (t.j. s = s₀ + r. (ϕ- ϕ₀)) resp. Δϕ = Δs/r (Pochopiteľne mimochodom platí aj všeobecne platný vzorec s= $\textstyle s_{0}\pm \int \limits _{t_{0}}^{t}|{\boldsymbol {v}}|\,\mathrm {d} {\bar {t}}$)
  1. Toto vyplýva zo všeobecne platného vzorca pre kruhový výsek.
  2. Ak ϕ nemeriame v radiánoch, ale v stupňoch, tak platí Δs = r. Δϕ.2.π /360°.
  3. V prípade celého jedného obehu (Δs = 2.π.r) je Δϕ = 2.π v radiánoch (resp. Δϕ = 360° v stupňoch).
  4. Vzorec s= $\textstyle s_{0}\pm \int \limits _{t_{0}}^{t}|{\boldsymbol {v}}|\,\mathrm {d} {\bar {t}}$ vyplýva z |v|=ds/dt
• |v| = v_d = r.(dϕ/dt) = r.ω (Keďže presnejšie je +/-|v| = v_d, tak presnejšie by malo byť: |v| =|v_d| = |r.(dϕ/dt)| = |r.ω|)
  v_d = r.(dϕ/dt) vyplýva zo spojenia vzorcov v_d=ds/dt a Δs = r.Δϕ
• |a_t| = a_d = r.(d²ϕ/dt) = r.α (Keďže presnejšie je +/- |a_t| = a_d, tak presnejšie by malo byť: |a_t| = |a_d| = |r.(d²ϕ/dt)| = |r.α|)
  |a_t| = r.(d²ϕ/dt) vyplýva zo spojenia vzorcov|a_t| = a_d , a_d = dv_d/dt a v_d = r.dϕ/dt
• |a_n| =v_d²/r = r.ω² = v_d.ω
  |a_n| =v_d²/r vyplýva z |a_n| = v_d²/R, ostatné je dosadené zhora
• |a| =$\textstyle {\sqrt {|{\boldsymbol {a}}_{t}|^{2}+|{\boldsymbol {a}}_{n}|^{2}}}$= $\textstyle r\cdot {\sqrt {\alpha ^{2}+\omega ^{4}}}$
  Prvý vzorec vyplýva zo vzorca pre skladanie vektorov zvierajúcich pravý uhol, druhý z dosadenia |a_t| a |a_n|.
• r = (r.cosϕ, r.sinϕ)
  Toto vyplýva zo vzorca pre cos a pre sin v pravouhlom trojuholníku, ak je referenčný polohový vektor (teda polohový vektor s ϕ=0) x-osová os.
• v = r.ω.τ =v_d.τ=ω x r
  Vzorec v = r.ω.τ vyplýva zo spojenia vzorcov v=dr/dt a r = (r.cosϕ, r.sinϕ). Vzorec v = ω x r dostaneme tak, že do v = r.ω.τ dosadíme vzorec τ = τ_ω x (-τ_n), čo je všeobecný vzorec pre prípady, keď vektory majú takú vzájomnú polohu, akú majú v našom prípade vektory τ, τ_ω a (-τ_n).
• a_t = r.α.τ = α x r (presnejšie: a_t = |r.α|.τ)
  Pozri nižšie pre a.
• a_n = r.ω². τ_n = -r.ω² = v_d.ω. τ_n =(v_d²/r).τ_n = ω x v= ω x (ω x r)
  Pozri nižšie pre a.
• a = r. α.τ + r.ω².τ_n = r. α.τ -r.ω² = r. α.τ + v_d.ω.τ_n = r. α.τ + (v_d²/r).τ_n =(α x r)+(ω x v)=(α x r)+(ω x (ω x r)) (presnejšie je vo vzorcoch |r.α| namiesto r. α)
  Prvé tri vzorce vyplývajú z a = dv/dt alebo alternatívne z a = a_t + a_n = |a_t|.τ + |a_n|.τ_n (V druhom vzorci je využitý vzťah r. τ_n = -r). Vzorec a=(α x r)+(ω x v) je výsledok výpočtu a=d(ω x r)/dt a následného dosadenia α = dω/dt a v=dr/dt (Vektorový súčin sa derivuje podľa vzorca pre deriváciu normálneho súčinu, ale namiesto znaku „.“ je vo vzorci znak „x“ a na rozdiel od derivácie normálneho súčinu sa musí dodržať poradie výrazov). V poslednom vzorci bolo už len dosadené v = ω x r
• ω = ω. τ_ω = (1/r²).(r x v)
  Prvý vzorec je všeobecné vyjadrenie vektora ako súčinu jeho veľkosti a jednotkového vektora. Vzorec ω = (1/r²).(r x v) vyplýva zo vzorca v = ω x r.
• α = α. (+/-τ_ω)= (1/r²).(r x a) = (1/r²).(r x ((α x r)+(ω x (ω x r)))
  Prvý vzorec je všeobecné vyjadrenie vektora ako súčinu jeho veľkosti a jednotkového vektora. Vzorec α = (1/r²).(r x a) je výsledok výpočtu α =d((1/r²).(r x v))/dt (t.j. α = (1/r²).(d(r x v)/dt)) a následného dosadenia v=dr/dt a a=dv/dt. V poslednom vzorci bolo už len dosadené a = (α x r)+(ω x (ω x r)

Podtypy

Tak ako každý pohyb hmotného bodu, aj pohyb hmotného bodu po kružnici možno rozdeliť na rovnomerný pohyb, rovnomerne premenný pohyb a nerovnomerne premenný pohyb (pričom výraz nerovnomerný pohyb je v širšom zmysle súhrnné označenie pre rovnomerne premenný a nerovnomerne premenný pohyb a v užšom zmysle len označenie pre nerovnomerne premenný pohyb).

Rovnomerný pohyb po kružnici

Iné názvy: pohyb po kružnici s konštantnou uhlovou rýchlosťou, pohyb po kružnici s konštantnou veľkosťou (obvodovej) rýchlosti [t.j. pohyb po kružnici s konštantnou dráhovou rýchlosťou]

Výraz “rovnomerný” (teda “konštantnú veľkosť rýchlosti majúci”) v názve tohto pohybu sa dá vztiahnuť tak na uhlové ako aj na obvodové veličiny, pretože tento pohyb je definovaný ako pohyb, pri ktorom platí:

• z hľadiska uhlových veličín je ω (resp. ω) konštantné (čiže ω = ω₀, inak povedané α = 0) resp.
• z hľadiska obvodových veličín je |v| (t.j. v_d) konštantné (čiže v_d=v_d,0, inak povedané |a_t|=0) a |a_n| je tiež konštantné.

Celkovo má tento pohyb tieto vlastnosti (porov. aj vzorce nižšie):

• uhlové veličiny:
  • ω (čiže|ω|) a ω je konštantné (čiže ide o pohyb s konštantnou veľkosťou uhlovej rýchlosti a pohyb s konštantnou uhlovou rýchlosťou)
  • α = 0, α je nulové
• obvodové veličiny:
  • |v| (čiže v_d) je konštantné, ale v sa mení (čiže ide o pohyb s konštantnou veľkosťou (obvodovej) rýchlosti [t.j. s konštantnou dráhovou rýchlosťou], ale s meniacou sa (obvodovou) rýchlosťou)
  • |a_t|=0 (čiže a_d =0), a_t je nulové
  • |a| (= |a_n|) je konštantné, ale a (=a_n) sa mení

Pre skalárne veličiny platí:

• ϕ = ϕ₀ + ω₀.Δt
  Toto vyplýva z integrovania vzorca ω=dϕ/dt ak je ω konštantné
• ω = ω₀=Δϕ/Δt =2π/T = 2πf (ak ϕ₀ = 0: ω = ω₀= ϕ/Δt)
  ω = ω₀ je východiskový predpoklad. Vzorec ω₀= Δϕ/Δt je len úprava vzorca ϕ = ϕ₀ + ω₀.Δt (ale vyplýva aj logicky z predpokladu, že ω je konštantné). Vzorec ω₀=2π/T vyplýva zo spojenia vzorcov ω₀= Δϕ/Δt a Δϕ = Δs/r a Δs=2πr a Δt=T. Vzorec ω₀=2πf vyplýva zo spojenia vzorcov ω₀=2π/T a f=1/T.
• α=0
  Toto je východiskový predpoklad.
• |v| = |v₀| =v_d = v_d,0 =r. ω₀ =2πr/T = Δs/Δt (Keďže presnejšie je +/-|v| = v_d, tak presnejšie by malo byť: |v| = |v_d| = |v_d,0| =|r. ω₀| =|2πr/T| = |Δs|/Δt )
  Vzorec v_d = v_d,0 =r. ω₀ vyplýva zo spojenia vzorcov v_d = r. ω a ω = ω₀ . Vzorec v_d =2πr/T vyplýva buď zo spojenia vzorcov v_d = r. ω₀ a ω₀=2π/T, alebo z integrovania vzorca v_d=ds/dt, čím dostaneme v_d,0=Δs/Δt (teda v_d,p), a následného dosadenia Δs=2πr a Δt=T. Vzorec |v| = |Δs|/Δt platí všeobecne pre pohyb s konštatným |v|.
• |a_t| =a_d = 0
  Keďže |a_t| = r.α a α= 0.
• |a_n|=|a_n,0|= v_d,0²/r=r.ω₀²=v_d,0.ω₀
  Vzorec sme získali dosadením v_d,0 a ω₀ do vyššie uvedených vzorcov pre |a_n|.
• |a| =|a₀| = |a_n|
  Toto je dosadenie do vzorca |a| =$\textstyle {\sqrt {|{\boldsymbol {a}}_{t}|^{2}+|{\boldsymbol {a}}_{n}|^{2}}}$= $\textstyle r\cdot {\sqrt {\alpha ^{2}+\omega ^{4}}}$.
• s = s₀ + r. ω₀.Δt = s₀ + |v₀|.Δt (presnejšie: s=s₀+/-r.ω₀.Δt=s₀+/-|v₀|.Δt)
  Vzorec s = s₀ + r. ω₀.Δt vyplýva zo spojenia vzorcov s = s₀ + r. (ϕ- ϕ₀) a ϕ = ϕ₀ + ω₀.Δt. Vzorec s =s₀ + |v₀|.Δt vyplýva z následného dosadenia vzorca|v₀|=r. ω₀, ale možno ho alternatívne odvodiť aj ako všeobecne platný vzorec pre rovnomerný pohyb (t.j. pre ľubovoľný pohyb s konštantným |v|).

Rovnomerne premenný (t.j. rovnomerne zrýchlený alebo spomalený) pohyb po kružnici

Iné názvy: pohyb po kružnici s konštantným uhlovým zrýchlením, pohyb po kružnici s konštantnou veľkosťou tangenciálneho zrýchlenia [t.j. pohyb po kružnici s konštantným dráhovým zrýchlením]:

Výraz “rovnomerne premenný” v názve tohto pohybu sa dá vztiahnuť tak na uhlové ako aj na obvodové veličiny, pretože tento pohyb je definovaný ako pohyb, pri ktorom platí:

• z hľadiska uhlových veličín je α (resp. α) konštantné a nenulové (čiže α = α₀ ≠0), resp.
• z hľadiska obvodových veličín je |a_t|(čiže a_d) konštantné a nenulové (čiže |a_t| = |a_t,0|≠0 resp. a_d =a_d,0 ≠0).

Celkovo má tento pohyb tieto vlastnosti (porov. aj vzorce nižšie):

• uhlové veličiny:
  • ω (čiže|ω|) a ω sa mení
  • α a α je konštantné a nerovné nule (čiže ide o pohyb s konštantnou veľkosťou uhlového zrýchlenia a pohyb s konštantným uhlovým zrýchlením)
• obvodové veličiny:
  • |v| (čiže v_d) a v sa mení
  • |a_t| (čiže a_d) je konštantné a nerovné nule, ale a_t sa mení (čiže ide o pohyb s konštantnou veľkosťou tangenciálneho zrýchlenia [t.j. pohyb s konštantným dráhovým zrýchlením])
  • |a_n| a a_n sa mení
  • |a| a a sa mení

Ak je α >0 (t.j. vektory α a ω majú rovnakú orientáciu), hovoríme o rovnomerne zrýchlenom pohybe, v opačnom prípade o rovnomerne spomalenom pohybe.

Pred uvedením vzorcov, je najprv je potrebný nasledujúci úvodný výpočet: Integrovaním vzorca α = dω/dt dostaneme ω = ω₀ +α₀.Δt. Integrovaním vzorca ω = dϕ/dt (t.j. ω₀ +α₀.Δt = dϕ/dt) dostaneme ϕ = ϕ₀ + ω₀.Δt + α₀.Δt²/2. Spojením tohto posledného vzorca s predchádzajúcim vzorcom ω = ω₀ +α₀.Δt dostaneme ω =((ω₀²-2.α₀.ϕ₀) + 2.α₀. ϕ)^1/2.

Potom platí pre skalárne veličiny:

• ϕ = ϕ₀ + ω₀.Δt + (1/2).α₀.Δt² (resp. ak ω₀= ϕ₀ =0: ϕ = (1/2).α₀.Δt²)
  Odvodenie pozri vyššie.
• ω = ω₀ +α₀.Δt = ((ω₀²-2.α₀.ϕ₀) + 2.α₀. ϕ)^1/2 (resp. ak ω₀= ϕ₀ =0: ω = α₀.Δt =(2.α₀. ϕ)^1/2 (Okrem toho keďže ω nie je konštantné, tak ω ≠Δϕ/Δt [hoci naďalej platí ω = dϕ/dt])
  Odvodenie pozri vyššie.
• α= α₀≠0 (a teda aj α = Δω/Δt)
  Toto je východiskový predpoklad.
• |v| = v_d = r(ω₀+ α₀.Δt) =v_d,0 + |a_t,0|. Δt (Keďže presnejšie je +/-|v| = v_d a +/-|a_t|=a_d, tak presnejšie má byť |v| = |v_d| = |r(ω₀+ α₀.Δt)| =|v_d,0 +/- |a_t,0|. Δt|.Okrem toho, keďže |v| nie je konštantné, tak platí |v| ≠ Δs/Δt, resp. presnejšie |v| ≠ |Δs|/Δt [hoci naďalej platí |v|=ds/dt])
  Vzorec v_d = r(ω₀+ α₀.Δt) vyplýva zo spojenia vzorcov v_d=r. ω a ω = ω₀ +α₀.Δt. Vzorec v_d =v_d,0 + |a_t,0|.Δt vyplýva z dosadenia v_d=r. ω a |a_t| = r.α do v_d = r(ω₀+ α₀.Δt)).
• |a_t| = |a_t,0| (=a_d =a_d,0) = r. α₀ (Keďže presnejšie je +/-|a_t|=a_d, tak presnejšie má byť|a_t| = |a_t,0| (=|a_d| =|a_d,0|) = |r.α₀|. Okrem toho, keďže |a_t|je konštantné, tak platí |a_t|= Δ|v|/Δt, presnejšie |a_t|= |Δ|v||/ Δt)
  Keďže |a_t| = r.α a α= α₀.
• |a_n| =r.(ω₀ +α₀.Δt)²
  Toto vyplýva zo spojenia vzorcov|a_n| =r.ω² a ω = ω₀ +α₀.Δt.
• |a| =$\textstyle r\cdot {\sqrt {a_{0}^{2}+(\omega _{0}+\alpha _{0}\cdot \Delta t)^{4}}}$
  Toto je dosadenie do vzorca |a| =$\textstyle {\sqrt {|{\boldsymbol {a}}_{t}|^{2}+|{\boldsymbol {a}}_{n}|^{2}}}$= $\textstyle r\cdot {\sqrt {\alpha ^{2}+\omega ^{4}}}$).
• s = s₀ + r. ω₀.Δt + (1/2).r.α₀.Δt = s₀ + |v₀|.Δt + (1/2).|a_t,0|. Δt² (Presnejšie: s = s₀ +/- r. ω₀.Δt +/- (1/2).r.α₀.Δt = s₀ +/- |v₀|.Δt +/- (1/2).|a_t,0|. Δt²)

Vzorec s=s₀+r. ω₀.Δt+(1/2).r.α₀.Δt vyplýva zo spojenia vzorcov s = s₀ + r. (ϕ- ϕ₀) a ϕ = ϕ₀ + ω₀.Δt + (1/2).α₀.Δt². Vzorec s= s₀+|v₀|.Δt + (1/2).|a_t,0|. Δt² vyplýva z následného dosadenia vzorcov|v₀|=r. ω₀ a |a_t,0| = r. α₀, ale možno ho alternatívne odvodiť aj ako všeobecne platný vzorec pre rovnomerne premenný pohyb (t.j. pre ľubovoľný pohyb s konštantným |a_t |).

Nerovnomerne premenný (t.j. nerovnomerne zrýchlený alebo spomalený alebo zrýchlený a spomalený) pohyb po kružnici

Iné názvy: pohyb po kružnici s nekonštantným uhlovým zrýchlením, pohyb po kružnici s nekonštantnou veľkosťou tangenciálneho zrýchlenia [t.j. pohyb po kružnici s nekonštantným dráhovým zrýchlením], nerovnomerný pohyb po kružnici [v užšom zmysle]

Výraz “nerovnomerne premenný” v názve tohto pohybu sa dá vztiahnuť tak na uhlové ako aj na obvodové veličiny, pretože tento pohyb je definovaný ako pohyb, pri ktorom platí:

• z hľadiska uhlových veličín je α (resp. α) nekonštantné a nenulové, resp.
• z hľadiska obvodových veličín je |a_t|(čiže a_d) nekonštantné a nenulové.

Nerovnomerne premenný pohyb po kružnici je teda každý pohyb po kružnici, ktorý nie je ani rovnomerný pohyb po kružnici, ani rovnomerne premenný pohyb po kružnici. Platia teda vždy „opaky“ vzorcov uvedených pod týmito dvoma pohybmi (nižšie označené ako A pre rovnomerný pohyb a B pre rovnomerne premenný pohyb).

• (A) ϕ ≠ ϕ₀ + ω₀.Δt; (B) ϕ ≠ ϕ₀ + ω₀.Δt + (1/2).α₀.Δt²
• (A) ω ≠ ω₀ (a teda ω ≠Δϕ/Δt [hoci naďalej platí ω = dϕ/dt]); (B) ω ≠ ω₀ +α₀.Δt, čiže ω ≠ ((ω₀²-2.α₀.ϕ₀) + 2.α₀. ϕ)^1/2
• (A) α ≠0; (B) α ≠ α₀ (a teda α ≠ Δω/Δt [hoci naďalej platí α = dω/dt])
• (A) |v| ≠ |v₀| (a teda |v|≠ Δs/Δt , presnejšie |v|≠ |Δs|/Δt [hoci naďalej platí |v|=ds/dt], a |v|≠ r. ω₀); (B) |v| ≠ v_d,0 + |a_t,0|. Δt, čiže |v| ≠ r(ω₀+ α₀.Δt) (presnejšie: |v| ≠ |v_d,0 +/- |a_t,0|. Δt|, t.j. |v| ≠ |r(ω₀+ α₀.Δt)|)
• (A) |a_t|≠0; (B) |a_t| ≠ |a_t,0| (a teda |a_t| ≠ Δ|v|/Δt, presnejšie |a_t|≠ |Δ|v||/ Δt [hoci naďalej platí |a_t|=d|v|/dt]), čiže |a_t| ≠ r. α₀ (presnejšie |a_t| ≠ |r. α₀|)
• (A) |a_n|≠|a_n,0|, čiže |a_n|≠ v_d,0²/r, |a_n|≠ r.ω₀², |a_n|≠ v_d,0.ω₀; (B) |a_n|≠r.(ω₀ +α₀.Δt)²
• (A) |a|≠|a₀|, čiže |a|≠|a_n|; (B) |a| ≠ =$\textstyle r\cdot {\sqrt {a_{0}^{2}+(\omega _{0}+\alpha _{0}\cdot \Delta t)^{4}}}$
• (A) s ≠ s₀ + r. ω₀.Δt, čiže s ≠ s₀ + |v₀|.Δt (presnejšie: s ≠ s₀ +/- r. ω₀.Δt, čiže s ≠ s₀ +/- |v₀|.Δt); (B) s ≠ s₀ + r. ω₀.Δt + (1/2).r.α₀.Δt, čiže s ≠ s₀ + |v₀|.Δt + (1/2).|a_t,0|. Δt² (presnejšie: s ≠ s₀ +/- r. ω₀.Δt +/- (1/2).r.α₀.Δt ≠ s₀ +/- |v₀|.Δt +/- (1/2).|a_t,0|. Δt²)

Silové pôsobenie (Kinetika)

Newtonove pohybové zákony

Pohyb po kružnici patrí medzi pohyby, pri ktorých je a≠ 0. Podľa 2. Newtonovho pohybového zákona (v jeho variante pre konštantnú hmotnosť) platí F = m.a (kde F je sila, m je hmotnosť, pričom m je konštatné a >0). Z tohto vyplýva, že pri pohybe, pri ktorom a≠0 (napr. pri pohybe po kružnici), musí byť aj F≠0, čiže musí na hmotný bod pôsobiť nejaká (výsledná) sila (Táto veta je vlastne zároveň istá forma formulácie 1. Newtonovho pohybového zákona).

Tangenciálna a dostredivá sila

Tak ako a môžeme rozložiť na tangenciálne (či dotyčnicové) a normálové (či dostredivé) zrýchlenie (a = a_t + a_n), tak (keďže F = m.a) aj F môžeme rozložiť na tangenciálnu (či dotyčnicovú) silu a normálovú (či dostredivú) silu (F = F_t + F_n = m.a_t + m.a_n). Konkrétnejšie dostaneme:

• F_t = m.a_t =m. (d|v|/dt).τ (resp. pre veľkosť sily: |F_t|=m.|a_t| = m. (d|v|/dt) )
• F_n = m.a_n =m. |v|.dτ/dt =m. (|v|²/R). τ_n (resp. pre veľkosť sily: |F_n|=m.|a_n| =m.(|v|²/R))

Keďže tangenciálne zrýchlenie sa týka iba zmeny veľkosti rýchlosti (t.j. zmeny |v|) a normálové zrýchlenie iba zmeny smeru a orientácie rýchlosti (t.j. zmeny τ), tak aj tangenciálna sila je sila, ktorá spôsobuje iba zmenu veľkosti rýchlosti a normálová sila je sila, ktorá spôsobuje iba zmenu smeru a orientácie rýchlosti. Celková sila, teda súčet tangenciálnej a normálovej rýchlosti, potom teda spôsobuje zmenu aj veľkosti aj smeru a orientácie rýchlosti hmotného bodu. Smer a orientácia F_t je rovnaký/-á ako smer a orientácia a_t (čiže smer majú rovnaký ako v, pri zrýchlenom pohybe majú aj rovnakú orientáciu ako v, ale pri spomalenom pohybe majú opačnú orientáciu ako v) a smer a orientácia F_n je rovnaký/-á ako smer a orientácia a_n (čiže kolmo na v s orientáciou dovnútra oblúka krivky pohybu, presnejšie: dovnútra oskulačnej kružnice).

Vyššie uvedené vzorce možno zjednodušiť či konkretizovať pre niektoré druhy pohybov: Pri priamočiarom pohybe (ktorý nie je predmetom tohto článku), t.j. pri pohybe, kde a_n je nulový vektor, je logicky F_n=0. Pri rovnomernom pohybe (napr. aj po kružnici), t.j. pri pohybe kde a_t je nulový, je logicky F_t =0. Pri (akomkoľvek) pohybe po kružnici zas platí po dosadení vzorcov pre a_t a a_n:

• F_t = m. r.α.τ = m.(α x r) (resp. pre veľkosť sily: |F_t|=m. r.α = m.(α x r)/τ)
• F_n = m. (|v|²/r). τ_n = m. r.ω². τ_n = m. (ω x (ω x r)) (resp. pre veľkosť sily: |F_n| = m. (|v|²/r) = m. r.ω²= m. (ω x (ω x r))/τ_n)

Odstredivá sila

K dostredivej sile (F_n) existuje v niektorých situáciách opačná sila. Táto sila s rovnakou veľkosťou (|F_n|) a smerom ale s opačnou orientáciou (-τ_n) než dostredivá sila sa nazýva odstredivá sila či centrifugálna sila ( -F_n). Ako sila pôsobiaca na samotný pohybujúci sa hmotný bod (teleso) je to len fiktívna sila; príkladom môže byť sila z pohľadu osoby sediacej na kolotoči. Ako sila pôsobiaca na „susedné“ hmotné body (telesá) je to reálna skutočná sila, ktorá je výsledkom zákona akcie-reakcie; príkladom môže byť sila, ktorou pôsobí vlak v zatáčke na koľajnice.

Fiktívna sila sa na odlíšenie od skutočnej sily niekedy označuje aj ako zotrvačná odstredivá sila.

Moment sily a zotrvačnosti

V kontexte pohybu po kružnici či otáčavého pohybu sa niekedy pracuje s veličinami moment sily a moment zotrvačnosti. Podobne ako sú uhlové veličiny ekvivalentmi „normálnych“ (t.j. obvodových) veličín, tak aj moment sily je ekvivalent sily (F) a moment zotrvačnosti je ekvivalent hmotnosti (m) pri otáčavom pohybe. Podrobnosti pozri v samostatných článkoch.

Zdroje

• prvé kapitoly:
  • MEYER, Heinz, et al.. Technische Mechanik (Teil 2: Kinematik und Kinetik). 7. vyd. Stuttgart : G G Teubner, 1991. ISBN 978-3-519-16521-7. S. 39-46.
  • OŽVOLDOVÁ, Miroslava; ČERVEŇ, Ivan. Úvod do vysokoškolskej fyziky. Bratislava : Slovenská technická univerzita, 2004. ISBN 80-227-2114-X. .s. 87-101
  • KRÁLÍK, Jiří. Mechanika – studijní text pro kombinované studium [online]. Katedra fyziky PF UJEP, 2007, [cit. 2016-08-25]. Dostupné online. Archivované 2017-04-14 z originálu. .s. 20-21
  • GÖBEL, Rudolf et al. "Fyzika pre maturantov". 2. vyd. Bratislava: Slovenské pedagogické nakladateľstvo, 1986. s. 106-109
  • KOKTAVÝ, Bohumil. "Mechanika hmotného bodu: učební text pro studenty distančního a denního studia". vyd. 2. v Akademickém nakl. CERM 1. Brno: Akademické nakladatelství CERM, 2006. Učební texty vysokých škol. ISBN 80-7204-474-5. s. 29-39
  • LEIFI Physik - Mechanik – Kreisbewegung - Grundwissen [online]. Joachim Herz Stiftung, [cit. 2016-08-30]. Dostupné online. Archivované 2016-08-28 z originálu.
• kapitola Silové pôsobenie (Kinetika):
  • BÖGE, Alfred, ed.. Vieweg Handbuch Maschinenbau. 18. vyd. Wiesbaden: Friedr. Vieweg und Sohn Verlag, 2007. ISBN 978-3-8348-0110-4. s. C60-C61.
  • AUTENRIETH. Ed. a ENSSLIN, M. Technische Mechanik (Ein Lehrbuch der Statik und Dynamik für Ingenieure). 3. vyd. Berlin: Verlag von Julius Springer, 1922. s. 268
  • Physik Online – Das E-Learning Portal des Fachbereichs Physik [online]. Universität Frankfurt, [cit. 2016-04-07]. Dostupné online. ^{[nefunkčný odkaz]}(Poznámka: Vo vzorci tangenciálnej sily je chyba)
  • ZAJÍC, Jan. Fyzika 1 [online]. Univerzita Pardubice – Fakulta chemicko-technologická, 2016, [cit. 2016-04-07]. Dostupné online. ^{[nefunkčný odkaz]}. s. 36, 68, 70-74
  • GÖBEL, Rudolf et al. Fyzika pre maturantov. 2. vyd. Bratislava: Slovenské pedagogické nakladateľstvo, 1986. s. 112-116
  • KLUVÁNEK, Peter. Pravda o odstredivej sile [online]. osel.cz, 2009, [cit. 2016-08-30]. Dostupné online.
  • REICHL, Jaroslav. Encyklopedie fyziky [online]. Jaroslav Reichl a Martin Všetička, [cit. 2016-08-25]. Dostupné online.

Pozri aj

• Pohyb (fyzika)
• Priamočiary pohyb