Projektívny priestor
V matematike je projektívny priestor množina prvkov podobná množine P(V) priamok prechádzajúcich počiatkom vo vektorovom priestore V. V špeciálnom prípade, ak V=R2 resp. V=R3, hovoríme o projektívnej priamke resp. projektívnej rovine.
Predstava o projektívnom priestore je podobná predstave o tom, ako oko alebo kamera zobrazuje 3D krajinu na 2D obrázok. Všetky body, ktoré ležia na premietacej priamke a pretínajú sa s ohniskovým bodom kamery sú zobrazené na spoločný bod obrázku.
Hoci tvoria projektívne priestory samostatnú časť matematiky, využívajú sa v mnohých ďalších aplikovaných oblastiach, najmä v diferenciálnej a algebrickej geometrii. Geometrické objekty, akými sú body, priamky a roviny, môžu byť pomocou homogénnych súradníc reprezentované prvkami v projektívnych priestoroch. Mnohé vzťahy medzi týmito objektmi tak môžu byť opísané jednoduchšou cestou a vety podané jednoduchšie (a bez výnimiek), než by tomu bolo bez homogénnych súradníc. Napríklad v klasickej geometrii sa dve priamky v konečnodimenzionálnom unitárnom priestore s definovaným štandardným skalárnym súčinom (t. j. v Euklidovskom priestore) vždy pretnú práve v jednom bode, s výnimkou, keď majú tieto priamky rovnaké zameranie (pre špeciálny prípad v rovine: ak sú tieto priamky rovnobežné, t. j. ak majú rovnakú smernicu). V projektívnej reprezentácii priamok a bodov takýto bod, v ktorom sa priamky pretínajú, existuje vždy a môže byť vypočítaný bežným postupom aj pre priamky s rovnakým zameraním.
Ďalšími odvetviami matematiky, v ktorých hrajú projektívne priestory významnú úlohu, sú topológia, teória Lieových grúp a algebrických grúp.
Úvod[upraviť | upraviť zdroj]
Pre lepšiu názornosť vytvoríme reálnu projektívnu rovinu P2(R3). Existujú najmenej tri ekvivalentné definície pre túto rovinu:
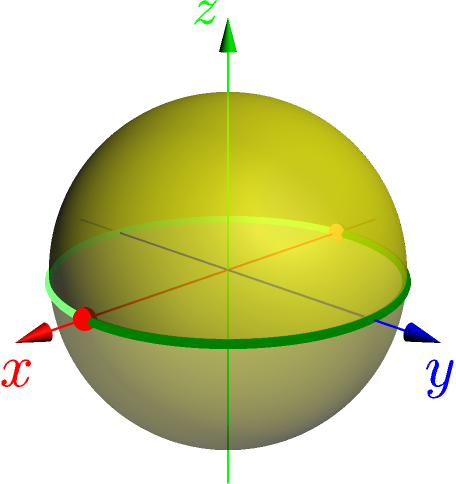
- Množina všetkých priamok v (reálnom 3D) priestore R3 prechádzajúcich cez počiatok (0,0,0). Každá taká priamka pretína sféru s polomerom jedna a stredom v počiatku práve dvakrát, povedzme v bode P = (x, y, z) a v protichodnom bode (-x, -y, -z).
- P2(R3) môže byť tiež opísaný pomocou bodov na sfére S2, kde každý bod P a jeho protichodný bod nie sú rozdielne. Napríklad bod (1, 0, 0) (červený bod na obrázku) je stotožnený s (-1, 0, 0) (svetlo červený bod), atď.
- Nakoniec, ešte ďalšou ekvivalentnou definíciou je, že P2(R3) je množina tried ekvivalencie priestoru R3\(0, 0, 0), t. j. 3-rozmerného priestoru bez počiatku, kde body P = (x, y, z) a Pˈ = (xˈ, yˈ, zˈ) sú ekvivalentné vtedy a len vtedy, ak existuje nenulové reálne číslo λ také, že P = λ·Pˈ, inými slovami x = λxˈ, y = λyˈ, z = λzˈ. Zaužívaný spôsob, akým sa zapisuje prvok projektívnej roviny, t. j. trieda ekvivalencie príslušná danému prvku (x, y, z) v R3, je
- [x : y : z].
Posledná formula sa zvykne uvádzať pod názvom homogénne súradnice.
Všimnime si, že každý bod [x : y : z] s z ≠ 0 je ekvivalentný s [x/z : y/z : 1]. Takže existujú dve disjunktné podmnožiny projektívnej roviny: tá, ktorá pozostáva z bodov [x : y : z] = [x/z : y/z : 1] pre z ≠ 0, a tá pozostávajúca zo zostávajúcich bodov [x : y : 0]. Tá druhá množina môže byť rozdelená podobne na dve disjunktné podmnožiny s bodmi [x/y : 1 : 0] a [x : 0 : 0]. V poslednom kroku, x je nevyhnutne nenulové, pretože počiatok nebol časťou P2(R3). Teda bod je ekvivalentný s [1 : 0 : 0]. Geometricky, prvá podmnožina, ktorá je izomorfná (nie iba ako množina, ale tiež ako varieta, ako uvidíme neskôr) s R2, je na obrázku žltá horná hemisféra (bez rovníka), alebo ekvivalentne dolná hemisféra. Druhá podmnožina, izomorfná s R1, sa zhoduje so zelenou priamkou (bez tých dvoch vyznačených bodov), alebo, znova, ekvivalentne, so slabo zelenou priamkou. Konečne, ostal nám červený bod, alebo ekvivalentne, svetlo červený bod. Máme tak disjunktný rozklad
- P2(R3) = R2 ⊔ R1 ⊔ bod.
Je už intuitívne jasné a rozobrané podrobnejšie ďalej v texte, že R1 ⊔ bod je reálna projektívna priamka P1(R2). Ak sa o nej uvažuje ako o podmnožine P2(R3), nazýva sa priamkou v nekonečne, kde R2 ⊂ P2(R3) sa nazýva afinná rovina, t. j. klasická rovina.

V ďalšom si objasníme obsah výroku: "rovnobežky sa pretínajú v nekonečne". Prirodzená bijekcia medzi rovinou z = 1 (ktorá pretína sféru na severnom póle N = (0, 0, 1)) a afinnou rovinou (t. j. spomínanou hornou hemisférou) vnútri projektívnej roviny je uskutočnená pomocou stereografickej projekcie, t. j. každý bod P na tejto rovine je zobrazený na bod, v ktorom sa pretína priamka prechádzajúca počiatkom a P so sférou. Preto dve priamky L1 and L2 (modré) na rovine sú zobrazené na niečo, čo vyzerá ako veľké kružnice (a teda protichodné body sú stotožnené). Veľké kružnice sa pretínajú presne na dvoch protichodných bodoch, ktoré sú v projektívnej rovine stotožnené, t. j. každé dve priamky sa pretínajú práve v jednom bode vnútri P2(R3). Tento jav je axiomatizovaný a skúmaný v projektívnej geometrii.
Definícia projektívneho priestoru[upraviť | upraviť zdroj]
Reálny projektívny priestor, Pn(Rn+1) je definovaný ako
- Pn(Rn+1) := (Rn+1 \ {0}) / ~,
s reláciou ekvivalencie (x0, ..., xn) ~ (λx0, ..., λxn), kde λ je ľubovoľné nenulové reálne číslo. Podobne je to tiež množina všetkých priamok v Rn+1 prechádzajúcich počiatkom 0 := (0, ..., 0).
Namiesto R, môžeme zobrať akékoľvek pole, alebo dokonca teleso k. Pre komplexné čísla alebo kvaternióny tak napríklad dostaneme komplexný projektívny priestor Pn(Cn+1) a kvaterniónový projektívny priestor Pn(Hn+1). V algebrickej geometrii sa projektívny priestor obvykle označuje ako Pnk.
Ak je n jednotka alebo dvojka, nazýva sa tiež projektívnou priamkou alebo projektívnou rovinou. Komplexná projektívna priamka je tiež nazývaná Riemannovou sférou.
Tak, ako v špeciálnom prípade uvedenom hore, označenie (nazývane homogénne súradnice) pre bod v projektívnom priestore je
- [x0 : ... : xn].
Všeobecnejšie, pre vektorový priestor V (nad nejakým poľom k, alebo ešte všeobecnejšie modul V nad nejakým telesom) je P(V) definované ako (V \ {0}) / ~, kde dva nenulové vektory v1, v2 z V sú ekvivalentné ak sa líšia len o nenulový skalár ?, t. j. ak v1 = ?·v2. Tento vektorový priestor nemusí byť konečne dimenzionálny, ako sa to používa napríklad v teórii projektívnych Hilbertových priestorov.
V teórii Alexandra Grothendiecka a špeciálne pri konštrukcii projektívnych fibrovaných priestorov (zvykne sa tiež používať pôvodné anglické pomenovanie bundle namiesto fibrovaný priestor), by sme chceli pridružiť projektívny priestor ku každému systému Y a každému kvázi-súdržnému snopu (angl. sheaf) E nad Y, nie iba k tým lokalne voľným. To sa dosiahne aplikovaním vyššie načrtnutých konštrukcií na duálny priestor V*. Viac detailov sa dá nájsť v pojednaní Éléments de géométrie algébriqueII, kapitola II, odsek 4.
Projektívny priestor ako varieta[upraviť | upraviť zdroj]

Z prv uvedenej definície vyplýva, že projektívny priestor tvorí množinu. Pre účely diferenciálnej geometrie, ktorá narába s varietami, je užitočné priradiť tejto množine štruktúru (reálnej alebo komplexnej) variety.
Zjednotenie podmnožín: tvorí podľa definície projektívneho priestoru celý projektívny priestor. Ďalej Ui tvorí bijekciu s Rn (alebo Cn) vzťahom
(tá strieška značí, že i-ty prvok chýba).
Obrázok ukazuje P1(R2). (Antipódne body v P1(R2) sú stotožnené). Je pokrytá dvoma kópiami reálnej priamky R a každá z nich pokrýva celú projektívnu priamku, okrem jedného bodu, ktorý je pomenovaný ako bod v nekonečne.
Topológiu na projektívnom priestore zadefinujeme tak, že tieto zobrazenia (mapy) vyhlásime za homeomorfizmus (nepliesť si s homomorfizmom), čo znamená, že podmožinu množiny Ui nazveme otvorenú vtedy a len vtedy, ak jej obraz (obor hodnôt) podľa už uvedeného izomorfizmu je otvorená podmnožina množiny Rn (vo zvyčajnom zmysle slova). Ľubovoľná podmnožina A z Pn(Rn+1) je otvorená ak všetky prieniky A ∩ Ui sú otvorené. To definuje topologický priestor.
Prv uvedenými zobrazeniami je vymedzená tiež štruktúra hľadanej variety.

Iný spôsob, akým možno premýšľať o projektívnej priamke je nasledujúci: urob dve samostatné kópie afinnej priamky so súradnicami x a y (v tomto poradí) a zlep ich spolu pozdĺž podmnožín x ≠ 0 a y ≠ 0 pomocou zobrazenia
Vzniknutá varieta je projektívna priamka. Schéma tejto konštrukcie je rovnaká ako tá, ktorá už bola uvedená vyššie. Podobný spôsob zobrazenia existuje aj pre viacrozmerné projektívne priestory.
Už uvedený rozklad na disjunktné podmnožiny je chápaný vo všeobecnosti takto:
- Pn(Rn+1) = Rn ⊔ Rn-1 ⊔ ⊔ R1 ⊔ R0.
Tento takzvaný rozklad na členy sa môže použiť na vypočítanie singulárnej kohomológie projektívneho priestoru.
Všetko, čo bolo napísané, platí samozrejme aj pre komplexné projektívne priestory. Komplexná projektívna priamka P1(C2) je príklad Riemannovej sféry.
Obsiahnutie pomocou uvedených otvorených podmnožín tiež ukazuje, že projektívny priestor je algebrická varieta (alebo tiež schéma): je obsiahnuta pomocou n + 1 afinných n-priestorov. Konštrukcia projektívnej schémy je príklad Proj konštrukcie.
Projektívne a afinné priestory[upraviť | upraviť zdroj]

Projektívne priestory majú oproti afinným priestorom určité výhody (napr. Pn(Cn+1) vs. Rn). Preto je užitočné vedieť, kedy je daná varieta projektívna, t. j. kedy sa vnára do (je uzavretá podmnožina) projektívneho priestoru. (Veľmi) rozsiahle fibrované priestory priamok sú vytvorené na riešenie tejto otázky.
- Projektívny priestor je kompaktný topologický priestor, afinný priestor taký nie je. V tejto súvislosti sa uvádza Liouvillov teorém, ktorý ukazuje, že každá holomorfná funkcia na Pn(Cn+1) je konštanta. Ďalší dôsledok je, že napríklad integrácia funkcií alebo diferenciálnych foriem na Pn neprináša konvergujúce výsledky.
- Na komplexnej projektívnej variete X, grupy kohomológií koherentných snopov F
H∗(X, F)
je konečne generovaná. (Príklad hore je (Pn(Cn+1), , nultá kohomológia snopu holomorfických funkcií). V reči algebrickej geometire je projektívny priestor vlastný. Všetky spomenuté výsledky platia aj v týchto súvislostiach. - Pre komplexný projektívny priestor, každá komplexná podvarieta X ⊂ Pn(Cn+1) (t. j., varieta vystrihnutá pomocou holomorfných rovníc) je nevyhnutne aj algebrickou varietou (t. j. určená polynomickými rovnicami). To sa nazýva Chowov teorém. Vďaka nemu možno použiť algebricko-geometrické metódy priamo aj pre tieto ad hoc analyticky definované objekty.
- Ako bolo naznačené vyššie, priamky v P2 či všeobecnejšie hyperroviny v Pn sa vždy pretínajú. Toto možno zovšeobecniť aj na nelineárne objekty: vhodne definujúc stupeň algebrickej krivky, ktorý je v podstate stupeň polynómov potrebných na definovanie krivky (pozri Hilbertov polynóm), stane sa pravdou (nad algebricky uzavretým telesom k), že každé dve projektívne krivky C1, C2 ⊂ Pkn stupňa e a f sa pretínajú presne v e·f bodoch, spočítajúc ich s viacnásobnými priesečníkmi (pozri Bézoutov teorém). Takto sa to používa napríklad pri definovaní grupovej štruktúry bodov eliptickej krivky, akou je napríklad y2 = x3-x+1. Stupeň eliptickej krivky je 3. Uvažujme priamku x = 1, ktorá sa pretína s krivkou (vnútri afinného priestoru) presne dvakrát, menovite v (1,1) a v (1,-1). Potom je projektívny uzáver krivky vnútri P2 určený homogénnou rovnicou
y2·z = x3-x·z2+z3,
ktorá pretína priamku (určenú vnútri P2 rovnicou x = z) v troch bodoch: [1: 1: 1], [1: -1: 1] (ktoré sa zhodujú s dvoma už vyššie spomenutými bodmi) a [0: 1: 0]. - Každá projektívna algebrická grupa, t. j. projektívna varieta, ktorej body tvoria abstraktnú grupu, je nevyhnutne aj abelovská varieta, t. j. grupová operácia je komutatívna. Eliptická krivka je príklad abelovskej variety. Komutativita zlyháva pre neprojektívne algebrické grupy, akou je napríklad GLn(k) (všeobecná lineárna grupa).
Axiómy pre projektívny priestor[upraviť | upraviť zdroj]
Projektívny priestor S môže byť definovaný abstraktne ako množina P (množina bodov) zjednotená s množinou podmnožín P (množinou priamok), ktorá je v súlade s axiómami:
- Každé dva body p and q, ktoré nie sú totožné, ležia presne na jednej priamke.
- Veblenov axióm: Ak a, b, c, d nie sú rozdielne body a priamky ab a cd sa pretínajú, potom majú túto vlastnosť aj priamky ac a bd.
- Každá priamka prechádza najmenej troma bodmi.
Posledný axióm nahrádza redukovateľné prípady, ktoré môžu byť napísané ako disjunktné zjednotenie projektívnych priestorov s 2-bodovými priamkami spájajúcimi akékoľvek dva body v disjunktných projektívnych priestoroch.
Podpriestor projektívneho priestoru je taká podmnožina X, že každá priamka obsahujúca dva body z X je podmnožina X. Tiež celý priestor a prázdny priestor sú podpriestory.
Geometrický rozmer priestoru za zvykne udávať ako n ak je to najväčšie číslo, pre ktoré existuje čiste stúpajúca postupnosť podmnožín v tejto forme:
Klasifikácia[upraviť | upraviť zdroj]

- Dimenzia 0 (žiadne priamky) Priestor tvorí jediný bod.
- Dimenzia 1 (Presne jedna priamka) Všetky body ležia na jedinej priamke.
- Dimenzia 2 (Najmenej 2 priamky a každé dve priamky sa pretínajú) Definícia projektívneho priestoru s číslom n = 2 je ekvivalentná s definíciou projektívnej roviny. Tieto sa ťažšie klasifikujú, keďže nie všetky sú izomorfné s PG(d, K). Desarguesovské roviny, pre ktoré platí Desarguesova veta, sú projektívne roviny nad telesom, ale existuje aj mnoho rovín, ktoré nie sú Desarguesovské.
- Dimenzia 3 a viac (2 nepretínajúce sa priamky) Veblena a Young (1965) dokázali Veblenov-Youngov teorém, ktorý hovorí, že ak je dimenzia n ≥ 3, každý projektívny priestor je izomorfný s PG(n, K), t. j. s n-rozmerným projektívnym priestorom nad nejakým telesom K.
Najmenšia projektívna rovina je Fanova rovina, PG[2,2] so 7 bodmi a 7 priamkami.
Morfizmus[upraviť | upraviť zdroj]
Injektívne lineárne zobrazenia T ∈ L(V,W) medzi dvoma vektorovými priestormi V a W nad nejakým poľom k indukujú zobrazenia korešpondujúcich projektívnych priestorov predpisom
kde v je nenulový prvok z V a […] označuje triedy ekvivalencie vektora. Keďže sa členy triedy ekvivalencie líšia o skalárny člen a lineárne zobrazenia zachovávajú skalárne členy, toto zobrazenie je dobre definované. (Ak T nie je injektívne, jeho jadro (niekedy sa tiež zvykne uvádzať pojem nulový priestor namiesto jadro) je väčšie než {0}; v tomto prípade je význam triedy T(v) problematický, ak je v nenulové a je prvkom jadra a získame takzvané racionálne zobrazenie.
Dve lineárne mapy S a T z L(V,W) tvoria rovnaké zobrazenie medzi P(V) a P(W) vtedy a len vtedy, ak sa líšia len o skalárny násobok, t. j. ak T=λS, kde λ ≠ 0. Ak stotožníme skalárne násobky identického zobrazenia s poľom, nad ktorým sa počíta, množina k-lineárnych morfizmov z P(V) do P(W) je jednoducho P(L(V,W)).
Zdroj[upraviť | upraviť zdroj]
- Tento článok je čiastočný alebo úplný preklad článku Projective space na anglickej Wikipédii.

![{\displaystyle U_{i}=\{[x_{0}:\cdots :x_{n}],x_{i}\neq 0\},i=0,\dots ,n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/907ca53b0985bf28ab590a73067d927d2272a16f)
![{\displaystyle [x_{0}:\cdots :x_{n}]\mapsto \left({\frac {x_{0}}{x_{i}}},\dots ,{\widehat {\frac {x_{i}}{x_{i}}}},\dots ,{\frac {x_{n}}{x_{i}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad19b5745f6950db50fec64d403797123dc4278)
![{\displaystyle [y_{0}:\cdots :y_{i-1}:1:y_{i+1}:\cdots y_{n}]\leftarrow (y_{0},\dots ,{\widehat {y_{i}}},\dots y_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5d03ae30c53b7e52a795f0c408988b002d94e7)





![{\displaystyle \mathbb {P} (V)\rightarrow \mathbb {P} (W),[\mathbf {v} ]\mapsto [T(\mathbf {v} )],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dc7a395c118b47aaae226b2d9c4b1d57315bc44)