Štandardný model
| Tento článok alebo jeho časť si vyžaduje úpravu, aby zodpovedal vyššiemu štandardu kvality. Prosím, pozrite si stránky pomocníka, odporúčanie pre encyklopedický štýl a článok vhodne upravte. |
Štandardný model fyziky častíc je zjednotený súbor teoretických poznatkov zahrňujúci väčšinu známych elementárnych častíc. V rámci modelu je možné zjednoteným spôsobom (zjednotenou matematickou formuláciou) popísať tri zo štyroch fundamentálnych interakcií: silnú, slabú, a elektromagnetickú. Štandardný model predstavuje relativistickú kvantovú teóriu vyhovujúcu zároveň princípom špeciálnej teórie relativity a kvantovej mechaniky. Gravitačné interakcie a teda ani všeobecná teória relativity nie su v modeli zahrnuté. Fundamentálnymi objektmi vystupujúcimi v tejto teórii sú polia v časopriestore, ktoré su metódou sekundárneho kvantovania prevedené na operátory.
Štandardný model bol vypracovávaný postupne. Jeho základy boli položené začiatkom 20. storočia. Súčasná formulácia bola dokončená v 70.-tych rokoch po experimentálnom potvrdení existencie kvarkov. Táto teória je v dobrom súlade so súčasnými experimentálnymi údajmi. Zahrňuje však 18 voľných parametrov, ktorých hodnotu nepredpovedá. Hodnota týchto parametrov je určená výhradne na základe experimentálnych výsledkov. Nepopisuje taktiež gravitáciu, tmavú hmotu či tmavú energiu. Nie je ani úplným popisom leptónov, pretože nepopisuje pozorovanú osciláciu neutrín (a teda ani nenulovú hmotnosť neutrín), i keď ich fenomenologický popis je v teórii zahrnutý.
Štandardný model je kalibračná teória silných (SU(3)) a elektroslabých (SU(2)×U(1)) interakcií s kalibračnou grupou (nazývanou tiež Štandardný model symetrickej grupy) SU(3)×SU(2)×U(1). Neberie do úvahy gravitáciu.
Historický vývoj[upraviť | upraviť zdroj]
V roku 1960 navrhol Sheldon Glashow teoretickú možnosť ako skombinovať elektromagnetickú a slabú interakciu do jednotnej teórie.[1] O sedem rokov neskôr doplnili Steven Weinberg[2] a Abdus Salam[3] navrhnutý teoretický model o Higgsov mechanizmus[4][5][6], ktorý priamo determinuje hmotnosti elementárnych častíc popísaných v rámci štandardného modelu. Špeciálne ide hlavne o hmotnosti W a Z bozónov a fermiónov. Higgsov mechanizmus takisto vysvetľuje, akým spôsobom "získavajú" hmotnosť kvarky a leptóny.
Po objave slabých neutrálnych prúdov v CERNe[7][8][9][10] spôsobených výmenou Z bozónov sa elektroslabá teória stala široko akceptovanou. Glashow, Salam a Weinberg, tvorcovia tejto teórie, následne dostali v roku 1979 Nobelovú cenu za fyziku. Neskôr, v r. 1981 boli experimentálne objavené bozóny W a Z. Experimentálne boli určené ich hmotnosti, pričom tieto boli v dobrej zhode s predpoveďami poskytnutými Štandardným modelom.
Teória silnej interakcie, získala svoju modernú podobu v rokoch 1973 – 74, kedy experimenty potvrdili, že hadróny sú zložené zo zlomkovo nabitých kvarkov.
Prehľad[upraviť | upraviť zdroj]
V súčasnosti sú hmota a energia najlepšie pochopené v pojmoch kinematiky a interakcií elementárnych častíc. Fyzikálne poznanie v súčasnosti smeruje k zredukovaniu fundamentálnych zákonitostí popisujúcich správanie sa a interakcie doteraz známych foriem hmoty a energie na čo najmenší súbor zákonov a teórií. Cieľom je nájsť takzvanú teóriu všetkého, ktorá by zjednotila všetky doteraz známe teórie do jednej jedinej integrovanej teórie. Predstavou je, že minimálne v princípe by z nej bolo možné odvodiť správane sa všetkej hmoty a energie[11] a že všetky doteraz známe zákony by boli špeciálnymi prípadmi takejto nadradenej teórie.
Štandardný model je vnímaný práve ako jeden z krokov k takejto zjednocujúcej teórii. Sú v ňom zahrnuté dve súčasné teórie – elektroslabá interakcia a kvantová chromodynamika. Štandardný model predstavuje vnútorne konzistentnú teóriu popisujúcu silné, slabé, a elektromagnetické interakcie medzi časticami v pojmoch kvantovej teórie poľa. Matematická formulácia štandardného modelu využíva kvantovanie fyzikálnych polí pomocou procesu nazývaného druhé kvantovanie.
Častice vystupujúce v štandardnom modeli[upraviť | upraviť zdroj]
Elementárne častice: fermióny[upraviť | upraviť zdroj]
| Náboj | Prvá generácia | Druhá generácia | Tretia generácia | ||||
|---|---|---|---|---|---|---|---|
| Kvarky | +2⁄3 | kvark u |
u | pôvabný kvark |
c | vrchný |
t |
| −1⁄3 | kvark d |
d | podivný kvark |
s | spodný |
b | |
| Leptóny | −1 | elektrón | mión | tauón | |||
| 0 | elektrónové neutríno | miónové neutríno | tauónové neutríno | ||||
Štandardný model obsahuje 12 elementárnych častíc so spinom 1⁄2 teda fermiónov. Fermióny podľa spinovo-štatistického teorému podliehajú Pauliho vylučovaciemu princípu. Každému fermiónu je priradená jeho zodpovedajúca antičastica.
Fermióny v štandardnom modeli klasifikujeme podľa interakcií, ktorým podliehajú (alebo ekvivalentne podľa nesených nábojov). Existuje šesť kvarkov (u, d, c, s, t, b a šesť leptónov, (elektrón, elektrónové neutríno, mión, miónové neutríno, tauón a tauónové neutríno). Páry z každej klasifikácie môžeme zoskupiť spoločne do jednej generácie. Pritom platí, že korešpondujúce si častice vykazujú podobné fyzikálne správanie (pozri tabuľku). Jednou z najdôležitejších vlastností kvarkov je, že nesú farebný náboj. Vďaka tomuto náboju interagujú medzi sebou prostredníctvom silnej interakcie. Efekt známy ako farebné uzavretie vysvetľuje skutočnosť, že kvarky nepozorujeme ako voľné častice, ale vždy navzájom viazané vo forme farebne neutrálnych častíc nazývaných hadróny. Hadróny sa skladajú buď z jedného kvarku a jedného antikvarku (mezóny) alebo z troch kvarkov (baryóny). Najznámejšími predstaviteľmi hadrónov sú protón a neutrón, ktoré sú zároveň najľahšími pozorovanými hadrónmi. Kvarky taktiež nesú elektrický a slabý náboj. Tieto vlastnosti vysvetľujú pozorované elektromagnetické a slabé interakcie s ostatnými fermiónmi.
Zvyšných šesť fermiónov nenesie žiaden farebný náboj a nazývajú sa leptóny. Tri z nich, nazývané neutrína, navyše nenesú ani elektrický náboj, takže interagujú výlučne len pomocou slabej interakcie. Z tohto dôvodu sú ťažko detegovateľné. Zvyšné tri leptóny, známe ako elektrón, mión a tauón nesú elektrický náboj. To znamená, že na rozdiel od neutrín interagujú navyše prostredníctvom elektromagnetickej interakcie.
Každý člen vyššej generácie má väčšiu hmotnosť ako korešpondujúce častice nižších generácií. Prvá generácia nabitých častíc sa nerozkladá; všetka obyčajná (baryonická) hmota pozostáva z týchto častíc. Konkrétne, všetky atómy pozostávajú z eletrónov a atómových jadier, ktorých nukleóny sú zložené z horných a dolných kvarkov. Druhá a tretia generácia nabitých častíc majú na druhej strane veľmi krátky polčas rozpadu a sú pozorované len vo veľmi vysoko energetických prostrediach. Neutrína všetkých generácií sa nerozkladajú a prenikajú celým vesmírom, ale zriedkakedy interagujú s baryonickou hmotou.
Intermediálne častice[upraviť | upraviť zdroj]
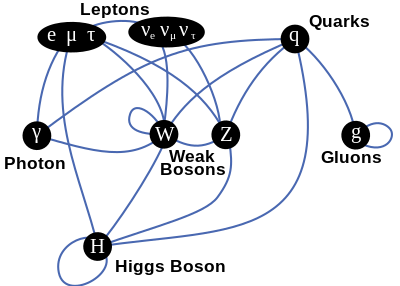
Vzájomné ovplyvňovanie sa častíc vo fyzike označujeme ako interakcie. Na makroskopickej úrovni popisujeme tieto interakcie pomocou polí. V prípade elektromagnetizmu sa tak deje prostredníctvom elektrických a magnetických polí. V prípade gravitácie popisujeme interakciu medzi hmotnými časticami v súlade s Einsteinovou všeobecnou teóriou relativity. V rámci Štandardného modelu však interpretujeme interakcie medzi časticami ako dôsledok neustáleho vzájomného si vymieňania iných vhodných častíc, ktoré dostali všeobecné pomenovanie intermediálne častice. Presnejšia interpretácia sa opiera o použitie aproximatívneho výpočtu interakcií známeho ako poruchová teória, ktorého grafickou reprezentáciou sú známe Feynmanove diagramy. Výmena intermediálnych častíc tak na makroskopickej úrovni vedie ku vzniku sily medzi časticami. V rámci teórie elementárnych častíc tak hovoríme, že intermediálne častice prenášajú silu, prípadne, že sú jej nositeľmi. Tento koncept je v dobrom súlade s dostupnými experimentálnymi údajmi. V prípade nízkoenergetickej kvantovej chromodynamiky (QCD), viazaných stavov častíc a solitónov však poruchová teória nedáva odpovede v súlade s nameranými hodnotami.
Jednou zo základných vlastností intermediálnych častíc popísaných v rámci štandardného modelu je spin. V prípade intermediálnych častíc je spin vždy rovný jednej. Z toho vyplýva, že intermediálne častice zaraďujeme medzi bozóny a riadia sa teda Boseho-Einsteinovou štatistikou. Jednotlivé intermediálne častice uvádzame v prehľade nižšie:
- Fotón prenáša elektromagnetickú silu medzi eletricky nabitými časticami. Fotón má v rámci Štandardného modelu hmotnosť rovnú nule. Jeho vlastnosti sú popísané v rámci kvantovej elektrodynamiky.
- W a Z bozóny prenášajú slabú interakciu. Podobne ako v prípade elektromagnetickej interakcie častice podliehajúce slabej interakcii nesú náboj, ktorý sa v tomto prípade nazýva vôňa (túto vlastnosť majú všetky kvarky a leptóny). W± bozóny majú hmotnosť približne 80,4 GeV/c2. Z0 bozón má hmotnosť približne 91,2 GeV/c2. Slabé interakcie zahŕňajúce W bozóny účinkujú výlučne na ľavotočivé častice a pravotočivé antičastice. W± bozóny nesú elektrický náboj a teda môžu interagovať pomocou elektromagnetickej interakcie. Elektricky neutrálny Z0 bozón interaguje tak s ľavočivými časticami ako aj s antičasticami. Tieto tri kalibračné bozóny spolu s fotónmi teda prenášajú elektroslabé interakcie.
- Gluóny prenášajú silnú interakciu. Nesú farebný náboj a majú nulovú hmotnosť. Existuje osem rozličných gluónov, ktoré rozlišujeme podľa neseného farebného náboja. Táto skutočnosť sa zvykne označovať termínom osemnásobná multiplicita. Zjednodušene môžeme hovoriť o tom, že gluóny nesú vždy farebný a antifarebný náboj a (napríklad červený-antizelený)[nb 1] Pretože gluóny nesú efektívny farebný náboj, môžu navzájom interagovať. Gluóny a ich vzájomné interakcie popisuje kvantová chromodynamika.
Interakcie medzi všetkými časticami v rámci Štandardného modelu sú prehľadne uvedené v obrázku navrchu tohto odseku.
Higgsov bozón[upraviť | upraviť zdroj]
Higgsov bozón je hypotetická hmotná skalárna častica, ktorú predpovedali v roku 1964 Robert Brout, Francois Englert, Peter Higgs, Gerald Guralnik, C. R. Hagen, a Tom Kibble. Prístup k mechanizmu spontánneho narušenia symetrie lokálnych kalibračných polí je v nimi publikovaných článkoch podobný s určitými rozdielmi (pozri PRL články o narušení symetrie). Mechanizmus spontánneho narušenia symetrie predstavuje kľúčový prvok v Štandardnom modeli.[12][13][14][15] )Štandardný model predpovedá spin Higgsovho bozónu rovný nule. Tak ako ostatné intermediálne častice s celočíselným spinom patrí medzi bozóny. Je to do dnešného dátumu jediná častica predpovedaná Štandardným modelom, ktorá nebola experimentálne objavená. Táto skutočnosť súvisí s potrebou vysokých energií a veľkej luminozity vo zväzkoch častíc zrážaných v urýchľovačoch častíc. V súčasnej dobe je Higgsov mechanizmus preverovaný experimentálne CERNe na Veľkom hadrónovom urýchľovači (LHC).
Higgsov bozón v rámci Štandardného modelu vysvetľuje, prečo majú ostatné elementárne častice s výnimkou fotónu a gluónu hmotnosť. Higgsov mechanizmus taktiež vysvetľuje, prečo fotón nemá hmotnosť, kým W a Z bozóny sú veľmi ťažké. Hmotnosti elementárnych častíc a rozdiely medzi elektromagnetizmom (prenášaným fotónom) a slabou silou (prenášanou W a Z bozónmi), sú zásadné pre mnoho aspektov mikroskopickej (a teda aj makroskopickej) štruktúry hmoty. V elektroslabej teórii interakcií generuje Higgsov bozón taktiež hmotnosť leptónov (elektrónu, miónu a tauónu) a kvarkov.
Polia vystupujúce v štandardnom modeli[upraviť | upraviť zdroj]
Štandardný model popisuje nasledujúce polia:
Spin 1[upraviť | upraviť zdroj]
- U(1) kalibračné pole Bμν s väzbovou konštantou g′ (slabá U(1) alebo slabý hypernáboj)
- SU(2) kalibračné pole Wμν s väzbovou konštantou g (slabá SU(2) alebo slabý izospin)
- SU(3) kalibračné pole Gμν s väzbovou konštantou gs (silná SU(3) alebo farebný náboj)
Spin 1⁄2[upraviť | upraviť zdroj]
Častice so spinom 1⁄2 sú uvedené v reprezentáciách kalibračnej grupy. Výnimkou je kalibračná grupa U(1), kde namiesto toho uvádzame hodnotu slabého hypernáboja. V štandardnom modely sú popísané nasledujúce ľavotočivé fermiónové polia:
- SU(3) triplet, SU(2) dublet s U(1) slabým hypernábojom 1⁄3 (ľavotočivé kvarky)
- SU(3) triplet, SU(2) singlet s U(1) slabým hypernábojom 2⁄3 (ľavotočivé antikvarky d)
- SU(3) singlet, SU(2) dublet s U(1) slabým hypernábojom −1 (ľavotočivý leptón)
- SU(3) triplet, SU(2) singlet s U(1) slabým hypernábojom −4⁄3 (ľavotočivé antikvarky u)
- SU(3) singlet, SU(2) singlet s U(1) slabým hypernábojom 2 (ľavotočivý antileptón)
K tomuto súboru ľavotočivých fermiónových polí existuje analogický súbor pravotočivých fermiónov s opačnými kvantovými číslami. Dôvodom je, že štandardný model nenarúša CPT symetriu.
Hore uvedený súbor opisuje len polia asociované s prvou generáciou kvarkov, teda s kvarkami d a u. Pre prípad druhej resp. tretej generácie kvarkov existuje analogický súbor polí. Dokopy teda obsahuje štandardný model tri súbory ľavotočivých fermiónov a tri súbory pravotočivých fermiónov, ktoré sú analogické hore uvedenému súboru polí.
Spin 0[upraviť | upraviť zdroj]
- SU(2) dublet H nesúci U(1) hypernáboj −1. Nazývame ho tiež Higgsovo pole.
Všimnite si tiež, že |H|2, napočítané cez dva SU(2) komponenty, je invariantné ako pod SU(2) tak pod U(1) a tak sa môže objaviť ako renormalizovateľný pojem v Lagrangiáne, rovnako ako jeho druhá mocnina.[chýba objasnenie]
Toto pole získava očakávanú vákuovú hodnotu, čo zabezpečuje, že kombinácia slabého izospinu, I3 a slabého hypernáboja zostáva neporušená. Toto je elektromagnetická kalibračná grupa a fotón zostáva nehmotný. Štandardný vzorec pre elektrický náboj (ktorý definuje normalizáciu slabého hypernáboja, Y, ktorý by bol ináč do istej miery arbitrárny) je:[nb 2]
Lagrangián[upraviť | upraviť zdroj]
Lagrangián pre polia typu spin 1 a spin 1⁄2 je najvšeobecnejšie renormalizačné Lagrangiánske kalibračné pole bez dolaďovania:
- Spin 1:
kde stopy sú nad SU(2) a SU(3) indexmi skryté v W resp. G. Dvojindexové objekty sú sily poľa odvodené od W a G vektorových polí. Existujú taktiež dva dodatočne skryté parametre: theta uhly pre SU(2) a SU(3).
Častice spinu 1⁄2 nemôžu mať pojem hmotnosti, pretože neexistuje žiaden pravo-ľavotočivý helicitný pár s rovnakými SU(2) a SU(3) zastúpeniami a rovnakým slabým hypernábojom. To znamená, že ak by kalibračné náboje boli konzervované vo vákuu, žiadna z častíc so spinom 1⁄2 by nebola schopná vymieňať si helicitu a boli by všetky nehmotné.
Pre neutrálny fermión napríklad, hypotetický pravotočivý leptón N (alebo Nα v relativistickej dvojspinorovej anotácii), bez SU(3), SU(2) zastúpenia a s nulovým nábojom, je možné pridať pojem:[chýba objasnenie]
Tento pojem dáva neutrálnemu fermiónu hmotnosť Majorana. Keďže obecná hodnota pre M bude mať stupeň 1, takáto častica by obecne bola neakceptovateľne ťažká. Interakcie sú úplne determinované teóriou – leptóny nezavádzajú žiadne dodatočné parametre.
Higgsov mechanizmus[upraviť | upraviť zdroj]
Lagrangián pre Higgsa zahŕňa najvšeobecnejšiu renormalizačnú samointerakciu:
Parameter v2 má rozmery hmotnosti na druhú a dáva umiestnenie, kde klasický lagrangián je na svojom minime. Ak má Higgsov mechanizmus fungovať, v2, musí byť pozitívne číslo. V má jednotky hmotnosti a je jediným parametrom v štandardnom modeli, ktorý nie je bezrozmerný. Je taktiež omnoho menší ako Planckova konštanta; rovná sa približne Higgsovej hmotnosti a stanovuje škálu pre hmotnosť všetkého ostatného. Toto je v štandardnom modeli jediné reálne jemné dolaďovanie na malú nenulovú hodnotu a nazýva sa hierarchický problém.
Tradične sa vyberá SU(2) kalibrácia, aby Higgsova dvojica vo vákuu mala očakávanú hodnotu (v,0).
Hmotnosti CKM matica[upraviť | upraviť zdroj]
Zvyšné interakcie sú vo všeobecnosti Yukawove interakcie spinom spin-0 spin-1⁄2, pričom ich existuje mnoho. Ustanovujú väčšinu voľných parametrov v modeli. Yukawove dvojičky generujú hmotnosti a zamiešanie ako Higgs dostáva svoje vákuovo očakávanú hodnotu.
Pojem L*HR[chýba objasnenie] generuje pojem hmotnosti pre každú z troch generácií leptónov. Existuje ich deväť, ale matica môže byť diagonalizovaná premenovaním L a R. Keďže len horný komponent H je nenulový, horný SU(2) komponent L sa mieša s R a vytvára elektrón, mión a tauón, pričom zanecháva nižší nehmotný komponent, neutríno.
Pojem QHU [chýba objasnenie] generuje hmotnosti s horným, kým QHD[chýba objasnenie] generuje hmotnosti s dolným spinom. Ale, keďže v každej generácii sa nachádza viac ako jeden pravotočivý samostatný jedinec, nie je možné diagonalizovať ako dobrú základňu pre polia a existuje tiež CKM matrica navyše.
Teoretické aspekty[upraviť | upraviť zdroj]
Konštrukcia Lagrangianského Štandardného modelu[upraviť | upraviť zdroj]
| Symbol | Opis | Renormalizačná schéma (point) |
Hodnota |
|---|---|---|---|
| me | Hmotnosť elektrónu | 511 keV | |
| mμ | Hmotnosť miónu | 106 MeV | |
| mτ | Hmotnosť tauónu | 1.78 GeV | |
| mu | Hmotnosť horného kvarku | μMS = 2 GeV | 1.9 MeV |
| md | Hmotnosť dolného kvarku | μMS = 2 GeV | 4.4 MeV |
| ms | Hmotnosť zvláštneho kvarku | μMS = 2 GeV | 87 MeV |
| mc | Hmotnosť pôvabného kvark | μMS = mc | 1.32 GeV |
| mb | Hmotnosť spodného kvarku | μMS = mb | 4.24 GeV |
| mt | Hmotnosť vrchného kvarku | On-shell scheme | 172.7 GeV |
| θ12 | CKM 12-zmiešaný uhol | 13.1° | |
| θ23 | 2.4° | ||
| θ13 | CKM 13-zmiešaný uhol | 0.2° | |
| δ | CKM CP-porušenie Phase | 0.995 | |
| g1 | U(1) kalibračné napojenie | μMS = mZ | 0.357 |
| g2 | SU(2) kalibračné napojenie | μMS = mZ | 0.652 |
| g3 | SU(3) kalibračné napojenie | μMS = mZ | 1.221 |
| θQCD | QCD vákuový uhol | ~0 | |
| μ | Higgsovo kvadratické napojenie | Neznáme | |
| λ | Higgsova samonapájacia sila | Neznáma |
Technicky, teória kvantového poľa poskytuje matematickú sústavu pre Štandardný model, v ktorom Lagrangián kontroluje dynamiku a kinematiku teórie. Každý druh častíc je popísaný pokiaľ ide o dynamické pole, ktoré preniká časopriestorom. Konštrukcia Štandardného modelu sleduje modernú metódu konštruovania väčšiny teórií polí: najprv postupuje súbor symetrií systému a potom popisuje najvšeobecnejší renormalizovateľný Lagrangián z jej obsahu častíc (poľa), ktoré dodržiavajú tieto symetrie.
Globálna Poincarého symetria je postulovaná pre všetky relativistické teórie kvantových polí. Pozostáva zo všeobecne známej translačnej symetrie, rotačnej symetrie a inertnej referenčnej rámcovej invariancie centrálnej pre teóriu špeciálnej relativity. Lokálna SU(3)×SU(2)×U(1) kalibračná symetria je interná symetria, ktorá v zásade definuje Štandardný model. Stručne, tri faktory kalibračnej symetrie dávajú vzniknúť trom fundamentálnym interakciám. Polia spadajú do rôznych zastúpení rôznych skupín symetrie Štandardného Modelu (pozri tabuľku). Po zapísaní najvšeobecnejších Lagrangianov zisťujeme, že dynamika závisí od 19 parameterov, ktorých numerické hodnoty sú ustanovené experimentom. Parametre sú zosumarizované v tabuľke napravo.
QCD sektor[upraviť | upraviť zdroj]
Elektroslabý sektor[upraviť | upraviť zdroj]
Pod pojmom elektroslabý sektor rozumieme v časticovej fyzike efekty súvisiace s elektroslabou interakciou. Tieto efekty sú v rámci štandardného modelu matematicky popísané symetrickou grupou U(1)×SU(2)L. Teória elektroslabej interakcie sa radí medzi kalibračné teórie Yang–Millsovho charakteru.
Matematická formulácia je založená na nasledujúcej Lagrangovej hustote:
kde značí kalibračné pole splňujúce U(1) symetriu; YW je slabý hypernáboj generujúci grupu U(1); označuje kalibračné pole o troch zložkách popísane grupou SU(2) ; sú Pauliho matice generujúce grupu SU(2); dolný index L znamená, že matice pôsobia len na ľavotočivé fermióny. Písmenami g′ a g sú označené väzbové konštanty.
Higgsov sektor[upraviť | upraviť zdroj]
V štandardom modeli, Higgsovo pole je komplexný spinor grupy SU(2)L:
kde indexy + and 0 indikujú elektrický náboj (Q) komponentov. Slabý izospin (YW) oboch komponentov je 1.
Pred porušením symetrie, Higgsov Lagrangian je:
čo sa tiež dá zapísať ako:
Dodatočné symetrie Štandardného modelu[upraviť | upraviť zdroj]
Z teoretického uhla pohľadu, Štandardný model vykazuje štyri dodatočné globálne symetrie, nepostulované pri náčrte ich konštrukcie, kolektívne označovaných ako náhodné symetrie, ktoré sú kontinuálnymi U(1) globálnymi symetriami. Transformácie dávajúce Lagrangianov invariant sú:
Prvým transformačným pravidlom je v skratke, že všetky kvarkové polia pre všetky generácie musia rotovať simultánne po identickej fáze. Polia , a , sú generácie druhého (mjuónu) and tretieho (tauónu) analogické k a poliam.
Podľa Noetherovej teorémy, každá vyššie uvedená symetria má asociovaný konzervačný zákon: konzerváciu baryónového čísla, elektrónového čísla, mjuónového čísla a tauónového čísla. Každý kvark má pridelené baryónové číslo 1/3, kým každý antikvark má pridelené baryónové číslo -1/3. Konzervácia baryónového čísla implikuje, že počet kvarkov mínus počet antikvarkov je konšstantný. V rámci experimentálneho limitu nebolo zistené žiadne porušenie tohto konzervačného zákona.
Podobne, každý elektrón a jeho pridelené neutríno má elektrónové číslo +1, kým antielektrón a jeho asociované antineutríno nesú elektrónové číslo −1. Podobne, mjuóny a ich neutrína majú pridelené mjuónové číslo +1 a tau leptóny majú pridelené tau leptónové číslo +1. Štandardný model predpovedá, že každé z týchto troch čísel by malo byť konzervované samostatne podobným spôsobom ako baryónové číslo. Tieto čísla sú kolektívne známe ako čísla leptónovej rodiny (LF). Symetria funguje ináč pre kvarky a ináč pre leptóny, hlavne kvôli tomu, že Štandardný model predpovedá, že neutríno je nehmotné. Ale, posledne bolo zistené, že neutrína majú malú hmotnosť a oscilujú medzi vôňami, signalizujúc, že konzervácia leptónovej rodiny je porušená.
Na dôvažok k náhodným (ale presným) symetriám popísaným vyššie, Štandardný model vykazuje niekoľko aproximovaných symetrií. Tieto sú tzv. "SU(2) uzatváracia symetria" a "SU(2) alebo SU(3) symetria kvarkovej vône."
| Symetria | Lieova skupina | typ symetrie | Konzervačný zákon |
|---|---|---|---|
| Poincaré | Translácie×SO(3,1) | Globálna symetria | Energia, Hybnosť, Uhlová hybnosť |
| kalibrácia | SU(3)×SU(2)×U(1) | Lokálna symetria | Farebný náboj, Slabý izospin, Elektrický náboj, Slabý hypernáboj |
| Baryónová fáza | U(1) | Náhodná Globálna symetria | Baryónové číslo |
| Elektrónová fáza | U(1) | Náhodná Globálna symetria | Elektrónové číslo |
| Mjuónová fáza | U(1) | Náhodná Globálna symetria | Mjuónové číslo |
| Tauónová fáza | U(1) | Náhodná Globálna symetria | Tauónové číslo |
| Field (1st generation) |
Spin | Kalibračná skupina Reprezentácia |
Baryón číslo |
Elektrón číslo | |
|---|---|---|---|---|---|
| ľavotočivý kvark | (, , ) | ||||
| Left-handed up antiquark | (, , ) | ||||
| Left-handed down antiquark | (, , ) | ||||
| Left-handed lepton | (, , ) | ||||
| Left-handed antielectron | (, , ) | ||||
| Hypercharge gauge field | (, , ) | ||||
| Isospin gauge field | (, , ) | ||||
| Gluon field | (, , ) | ||||
| Higgsovo pole | (, , ) | ||||
Zoznam fermiónov v Štandardnom modeli[upraviť | upraviť zdroj]
Táto tabuľa je založená na údajoch získaných Skupinou pre časticové dáta.[16]
| Generation 1 | |||||||
|---|---|---|---|---|---|---|---|
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Electron | 511 keV | ||||||
| Positron | 511 keV | ||||||
| Electron neutrino | < 2 eV **** | ||||||
| Antielectron neutrino | < 2 eV **** | ||||||
| Up quark | ~ 3 MeV *** | ||||||
| Up antiquark | ~ 3 MeV *** | ||||||
| Down quark | ~ 6 MeV *** | ||||||
| Down antiquark | ~ 6 MeV *** | ||||||
| Generation 2 | |||||||
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Muon | 106 MeV | ||||||
| Antimuon | 106 MeV | ||||||
| Muon neutrino | < 2 eV **** | ||||||
| Antimuon neutrino | < 2 eV **** | ||||||
| Charm quark | ~ 1.337 GeV | ||||||
| Charm antiquark | ~ 1.3 GeV | ||||||
| Strange quark | ~ 100 MeV | ||||||
| Strange antiquark | ~ 100 MeV | ||||||
| Generation 3 | |||||||
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Tauon | 1.78 GeV | ||||||
| Antitauon | 1.78 GeV | ||||||
| Tauon neutrino | < 2 eV **** | ||||||
| Antitauon neutrino | < 2 eV **** | ||||||
| Top quark | 171 GeV | ||||||
| Top antiquark | 171 GeV | ||||||
| Bottom quark | ~ 4.2 GeV | ||||||
| Bottom antiquark | ~ 4.2 GeV | ||||||
Poznámky:
- * Tieto nie sú obyčajné abelianske náboje, ktoré by bolo možné dať dohromady, ale známky skupinového zastúpenia Lieovej skupiny.
- ** Hmotnosť je v skutočnosti napojenie medzi ľavotočivým fermiónom a pravotočivým fermiónom. Napríklad, hmotnosť elektrónu je v skutočnosti napojenie medzi ľavotočivým elektrónom a pravotočivým elektrónom, ktorý je antičasticou ľavotočivého pozitrónu. Tiež neutrína vykazujú veľké premiešanie s ich hmotnostným partnerom, takže nie je správne hovoriť o hmotnostiach neutrín na zásade vôní, alebo to vysvetľovať ako ľavotočivé elektrónové antineutríno.
- *** Hmotnosť baryónov a hadrónov a rôznych priesečníkov sú experimentálne merané objemy. Keďže kvarky nemožno izolovať kvôli QCD uzatvoreniu, kvantita tu je podľa všetkého hmotnosť kvarku pri renormalizačnej škále QCD.
- **** Štandardný model predpokladá, že neutrína sú nehmotné. Ale, niekoľko súčasných experimentov dokazuje, že neutrína oscilujú medzi svojimi stavmi vôní, ktoré by nemohli existovať, ak by všetky boli nehmotné.[17] Model sa to priamo rozširuje, aby vyhovoval týmto údajom, ale existuje mnoho možností, takže hmotnosti eigenstavov sú stále otvorené.
Testy a predpovede[upraviť | upraviť zdroj]
Štandardný model (ŠM) predpovedal existenciu W a Z bozónov, gluónov a vrchného a kvarkov s vôňami predtým, ako boli tieto častice pozorované. Tieto predpovedané častice boli experimentálne potvrdené s dobrou presnosťou. Pre predstavu úspechu ŠM, nasledovná tabuľka porovnáva namerané hmotnosti W a Z bozónov s hmotnosťami predpovedanými ŠM-om:
| Quantity | Measured (GeV) | SM prediction (GeV) |
|---|---|---|
| Mass of W boson | 80.398 ± 0.025 | 80.390 ± 0.018 |
| Mass of Z boson | 91.1876 ± 0.0021 | 91.1874 ± 0.0021 |
ŠM taktiež robí niekoľko predpovedí o rozklade Z bozónov, ktoré boli experimentálne potvrdené Veľkým hadrónovým urýchľovačom v CERNe.
Problémy štandardného modelu[upraviť | upraviť zdroj]
| Tejto sekcii chýbajú odkazy na použité zdroje, obsah preto nie je možné overiť. |
Nevyriešené otázky:
- Čo dáva oprávnenia pre Štandardný model časticovej fyziky?
- Prečo sú hmotnosti častíc a napojovacej konštanty také aké sa namerali?
- Existuje Higgsov bozón?
- Prečo existujú tri generácie častíc?
Existuje istý experimentálny dôkaz konzistentný s neutrínami s hmotnosťou, ktorý Štandardný model nedovoľuje. Pre zakomponovanie takýchto zistení, Štandardný model môže byť modifikovaný pridaním nerenormalizovateľnej interakcie leptónových polí s Higgsovým poľom na druhú. Toto je prirodzené v istýchunifikačných teóriách a ak sa nová fyzika javí približne na úrovni okolo 1016 GeV, neutrínové hmotnosti sú správneho rozsahu magnitúdy.
V súčasnosti existuje jedna elementárna častica predpovedaná Štandardným modelom, ktorá ešte nebola pozorovaná: Higgsov bozón. Veľkým dôvodom pre vybudovanie LHC je, že vysoké energie, ktorých je schopný by mohli umožniť pozorovateľnosť Higgsovho bozónu. Ale, k aprílu 2010 existuje len nepriamy dôkaz pre existenciu Higgsovho bozónu, takže jeho objavenie nie je možné potvrdiť. Navyše, existujú vážne teoretické dôvody sa domnievať, že elementárny skalár Higgsovej častice nemôže existovať (pozri Kvantová trivialita).
Bol už urobený značný teoretický a experimentálny výskum na rozšírenie Štandardného modelu Veľkú unifikačnú teóriu alebo teóriu všetkého, úplnú teóriu vysvetľujúcu všetky fyzikálne javy vrátane konštánt. Neadekvátnosti Štandardného modelu, ktoré motivujú takýto výskum zahŕňajú:
- Nepokúša sa vysvetliť gravitáciu a neexistuje žiaden známy spôsob adaptácie teórie kvantového poľa druhu, ktorý Štandardný model voľne používa, so všeobecnou teória relativity, kanonickou teóriou gravitácie. To znamená, o. i., že nemáme žiadnu dobrú teóriu pre veľmi raný vesmír;
- Zdá sa dosť ad-hoc a neelegantnou, vyžadujúcou 19 číselných konštánt, ktorých hodnoty sú neprepojené a arbitrárne. Hoci Štandardný model, ak je to dnes, nedokáže vysvetliť, prečo majú neutrína hmotnosť (a špecifikácie neutrínovej hmotnosti sú stále nejasné), panuje obava, že vysvetlenie hmotnosti neutrína si budú vyžadovať dodatočných 7 až 8 konštánt;
- poskytuje dôvod pre hierarchický problém, totiž, prečo sú slabá škála a Planckova škála tak rozdielne;
- Mal by byť modifikovaný, aby bol v súlade s objavujúcou sa "kozmológiou Štandardného modelu." Konkrétne, skutočne uspokojivá teória elementárnych častíc a základných interakcií musí vysvetliť počiatočné podmienky vesmíru, ktoré zapríčinili isté pozorované vlastnosti súčasného vesmíru, vlastnosti ako prevládanie hmoty nad antihmotou (hmota/antihmota asymetria), a ich izotropia a homogenitu na veľké vzdialenosti.
Je potrebné poznamenať, že ani Unifikovaná teória poľa ani Teória všetkého nie sú v súčasnosti schopné vyjadriť sa k týmto problémom rozhodujúcim spôsobom.
Pozri aj[upraviť | upraviť zdroj]
- Elementárna častica:
- Základná interakcia:
- Kalibračná teória
- Otvorené otázky: BTeV experiment, CP porušenie, Neutrínová hmotnosť, Kvarková hmota
- kvantová teória poľa
- Štandardný Model:
- Diagramy:
- Vôňa
- Generácia
- Higgsov mechanizmus
- Higgsov bozón
- Prehľad a rozdiely štúdie z r. 1964 o PRL Porušení symetrie
- Lagrangian
- Nekomutatívny Štandardný model
- Cena J. J. Sakuraiho za teoretickú časticovú fyziku
Poznámky a referencie[upraviť | upraviť zdroj]
- Poznámky
- ↑ , technicky teda existuje deväť takýchto farebne-antifarebných kombinácií. Ďalšou požiadavkou však je, aby boli tieto stavy lineárne nezávislé a netvorili farebný singlet.
- ↑ Niekedy sa namiesto toho používa normalizácia Q = I3 + Y.
- Referencie
- ↑ S.L. Glashow. Partial-symmetries of weak interactions. Nuclear Physics, 1961, s. 579–588. DOI: 10.1016/0029-5582(61)90469-2.
- ↑ S. Weinberg. A Model of Leptons. Physical Review Letters, 1967, s. 1264–1266. DOI: 10.1103/PhysRevLett.19.1264.
- ↑ A. Salam, N. Svartholm: Elementary Particle Physics: Relativistic Groups and Analyticity. konferencia Eighth Nobel Symposium. Almquvist and Wiksell: Štokholm 1968.
- ↑ F. Englert, R. Brout. Broken Symmetry and the Mass of Gauge Vector Mesons. Physical Review Letters, 1964, s. 321–323. DOI: 10.1103/PhysRevLett.13.321.
- ↑ P.W. Higgs. Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters, 1964, s. 508–509. DOI: 10.1103/PhysRevLett.13.508.
- ↑ G.S. Guralnik, C.R. Hagen, T.W.B. Kibble. Global Conservation Laws and Massless Particles. Physical Review Letters, 1964, s. 585–587. DOI: 10.1103/PhysRevLett.13.585.
- ↑ F.J. Hasert et al.. Search for elastic muon-neutrino electron scattering. Physics Letters B, 1973, s. 121. DOI: 10.1016/0370-2693(73)90494-2.
- ↑ F.J. Hasert et al.. Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment. Physics Letters B, 1973, s. 138. DOI: 10.1016/0370-2693(73)90499-1.
- ↑ F.J. Hasert et al.. Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment. Nuclear Physics B, 1974, s. 1. DOI: 10.1016/0550-3213(74)90038-8.
- ↑ D. Haidt. The discovery of the weak neutral currents [online]. 4 October 2004, [cit. 2008-05-08]. Dostupné online.
- ↑ „Detaily je možné vypracovať, ak je situácia dostatočne jednoduchá, aby bolo možné urobiť aproximáciu, ku ktorej nedochádza takmer nikdy, ale často tak môžeme viac-menej pochopiť, čo sa deje“ z Feynmanove prednášky o fyzike, časť 1. s. 2 – 7
- ↑ F. Englert, R. Brout. Porušená symetria a hmotnosť kalibračných vektorových mezónov. Physical Review Letters, 1964, s. 321–323. DOI: 10.1103/PhysRevLett.13.321.
- ↑ P.W. Higgs. Porušená symetria a hmotnosti kalibračných bozónov. Physical Review Letters, 1964, s. 508–509. DOI: 10.1103/PhysRevLett.13.508.
- ↑ G.S. Guralnik, C.R. Hagen, T.W.B. Kibble. Globálne konzervačné zákony a nehmotné častice. Physical Review Letters, 1964, s. 585–587. DOI: 10.1103/PhysRevLett.13.585.
- ↑ G.S. Guralnik. História vývoja Guralnikovej, Hagenovej a Kibbleho theórie spontánneho porušenia symetrie a kalibračných častíc. International Journal of Modern Physics A, 2009, s. 2601–2627. DOI: 10.1142/S0217751X09045431. arXiv:0907.3466.
- ↑ W.-M. Yao et al. (Particle Data Group). Review of Particle Physics: Quarks. Journal of Physics G, 2006, s. 1. Dostupné online. DOI: 10.1088/0954-3899/33/1/001.
- ↑ W.-M. Yao et al. (Particle Data Group). Review of Particle Physics: Neutrino mass, mixing, and flavor change. Journal of Physics G, 2006, s. 1. Dostupné online.
Ďalšie čítanie[upraviť | upraviť zdroj]
Všeobecné čítanie[upraviť | upraviť zdroj]
- R. Oerter. The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. [s.l.] : Plume, 2006.
- B.A. Schumm. Deep Down Things: The Breathtaking Beauty of Particle Physics. [s.l.] : Johns Hopkins University Press, 2004. ISBN 0-8018-7971-X.
- V. Stenger. Timeless Reality. [s.l.] : Prometheus Books, 2000. pozri hlavne kapitoly 9 – 12.
Úvodné učebnice[upraviť | upraviť zdroj]
- I. Aitchison, A. Hey. Gauge Theories in Particle Physics: A Practical Introduction.. [s.l.] : Institute of Physics, 2003. ISBN 9780585445502.
- W. Greiner, B. Müller. Gauge Theory of Weak Interactions. [s.l.] : Springer, 2000. ISBN 3-540-67672-4.
- G.D. Coughlan, J.E. Dodd, B.M. Gripaios. The Ideas of Particle Physics: An Introduction for Scientists. [s.l.] : Cambridge University Press, 2006.
- D.J. Griffiths. Introduction to Elementary Particles. [s.l.] : John Wiley & Sons, 1987. ISBN 0-471-60386-4.
- G.L. Kane. Modern Elementary Particle Physics. [s.l.] : Perseus Books, 1987. ISBN 0-201-11749-5.
Pokročilé učebnice[upraviť | upraviť zdroj]
- T.P. Cheng, L.F. Li. Gauge theory of elementary particle physics. [s.l.] : Oxford University Press, 2006. ISBN 0-19-851961-3. Highlights the gauge theory aspects of the Standard Model.
- J.F. Donoghue, E. Golowich, B.R. Holstein. Dynamics of the Standard Model. [s.l.] : Cambridge University Press, 1994. ISBN 978-0521476522. Highlights dynamical and phenomenological aspects of the Standard Model.
- L. O'Raifeartaigh. Group structure of gauge theories. [s.l.] : Cambridge University Press, 1988. ISBN 0-521-34785-8. Highlights group-theoretical aspects of the Standard Model.
Články v časopisoch[upraviť | upraviť zdroj]
- E.S. Abers, B.W. Lee. Gauge theories. Physics Reports, 1973, s. 1–141. DOI: 10.1016/0370-1573(73)90027-6.
- Y. Hayato et al.. Search for Proton Decay through p → νK+ in a Large Water Cherenkov Detector. Physical Review Letters, 1999, s. 1529. DOI: 10.1103/PhysRevLett.83.1529.
- S. F. Novaes (2000). "Standard Model: An Introduction" arXiv: [1]
- D.P. Roy (1999). "Basic Constituents of Matter and their Interactions — A Progress Report.". arXiv: [2].
- F. Wilczek (2004). "The Universe Is A Strange Place". arXiv: [3]
Externé odkazy[upraviť | upraviť zdroj]
- "Standard Model - vysvetlenie pre začiatočníkov" LHC
- "Štandardný model je možno neúplný," New Scientist.
- "Pozorovania vrchného kvarku" vo Fermilabe.
- "The Standard Model Lagrangian. Archivované 2008-11-21 na Wayback Machine" Po porušení elektroslabej symetrie, bez explicitného Higgsovho bozónu.
- "Standard Model Lagrangian Archivované 2012-11-06 na Wayback Machine" s explicitnými Higgsovými pojmami. PDF, PostScript, and LaTeX versions.
- "The particle adventure." Web tutorial.
- Nobes, Matthew (2002) "Introduction to the Standard Model of Particle Physics" on Kuro5hin: Part 1, Part 2, Part 3a, Part 3b.
- [4] Youtube video o vývoji kozmologických predstáv v 2. pol. 20. storočia – od Štandardného modelu k teórii strún"
- [5] – Prednáška Stevena Weinberga Higgs, dark matter and supersymmetry: What the Large Hadron Collider will tell us










![{\displaystyle S_{\mathrm {Higgs} }=\int d^{4}x\left[(D_{\mu }H)^{*}(D^{\mu }H)+\lambda (|H|^{2}-v^{2})^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64569f95fe78a3adfc777864aa1de07c99bf759)





































































