Portál:Matematika/Odporúčané články/2006

2006

34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49

34 2006

Derivácia nejakej funkcie je zmena (rast) tejto funkcie v pomere k veľmi malej zmene jej premennej či premenných. Opačným procesom k derivovaniu je integrovanie.

Je to jeden ze základných pojmov matematiky, konkrétne diferenciálneho počtu.

Koncept derivácie sa dá intrepretovať rôznymi spôsobmi, napríklad v prípade dvojrozmerného grafu funkcie f(x), je derivácia tejto funkcie v ľubovoľnom bode (v ktorom existuje) rovná smernici dotyčnice tohto grafu. Z toho vidno, že sa pojem derivácie objavuje aj v mnohých geometrických súvislostiach, napr. pri pojme konkávnosť.

35 2006

Integrál je spolu s deriváciou najdôležitejší pojem matematickej analýzy. Pojem integrálu je zovšeobecnením pojmov ako plocha, objem, súčet či suma. Integrovanie je opačná operácia k derivovaniu.

Jednoducho povedané, určitý integrál nezápornej funkcie f(x) medzi nejakými dvoma bodmi a, b je rovný ploche obrazca ohraničeného priamkami x = a, x = b, osou x a krivkou definovanou funkciou f. Formálnejšie povedané, taký integrál je rovný miere množiny S definovanej ako

S=\{(x,y)\in \mathbb {R} ^{2}:a\leq x\leq b,0\leq y\leq f(x)\}.

Integrál sa označuje štylizovaným pretiahnutým písmenom S (z lat. summa). Toto značenie zaviedol matematik Gottfried Leibniz.

36 2006

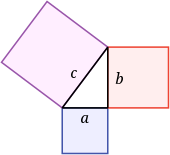
Pytagorova veta je základná teoréma euklidovskej geometrie. Popisuje vzťah, ktorý platí medzi dĺžkami strán pravouhlého trojuholníka v rovine. Umožňuje jednoducho vypočítať dĺžku tretej strany trojuholníka, ak sú známe dĺžky jeho dvoch zvyšných strán. Slovne sa veta dá formulovať takto:

obsah štvorca zostrojeného nad preponou (najdlhšou stranou) pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.

Formálne možno Pytagorovu vetu vyjadriť rovnicou

a^{2}+b^{2}=c^{2}

,

kde $a$ , $b$ sú dĺžky odvesien a $c$ je dĺžka prepony pravouhlého trojuholníka.

37 2006

Limita je v matematike hodnota, ku ktorej sa "približuje" premenlivá hodnota.

Limita funkcie sa používa na opis správania sa funkcie, keď sa jej argument "približuje" k nejakému bodu alebo rastie do nekonečna. Limity sa využívajú v matematickej analýze na definovanie derivácie a spojitosti.

Koncept "limity funkcie" sa dá ďalej zovšeobecniť na topologickú sieť a limita postupnosti úzko spojená s limitou a priamou limitou v teórii kategórií.

38 2006

revízia

Komplexné čísla sú zovšeobecnením pojmu reálne čísla. V obore reálnych čísel nemajú všetky polynomiálne rovnice riešenie. Ak zadefinujeme číslo i, ako riešenie rovnice $x^{2}=-1$ , tak všetky polynomiálne rovnice riešenie mať budú.

Väčšina ľudí pozná iba reálne čísla. Nachádzajú sa v jednom rade usporiadané podľa veľkosti. Tento rad reálnych čísel nazývame číselná os. Číselná os má rozmedzie od mínus nekonečna až po plus nekonečno. Keď si túto os predstavíme ako priamku, ktorá leží v rovine, logicky sa spýtame, či aj v iných bodoch roviny okrem bodov tejto priamky môžeme nájsť nejaké čísla.

Ukazuje sa, že áno. Aj v iných miestach roviny sa nachádzajú čísla. Tieto čísla nazývame imaginárne čísla. Dokopy so všetkými reálnymi číslami tvoria množinu všetkých komplexných čísel. Definoval ich nemecký matematik Gauss a podľa neho sa aj táto rovina čísel pomenovala Gaussova rovina. Túto rovinu rozdeľujú dve osi — už spomínaná číselná os, ktorú budeme pokladať za os x (reálna os) a na ňu kolmá os y (imaginárna os). Obe tieto osi sa pretínajú v bode [0;0].

39 2006

Carl Friedrich Gauss (* 30. apríl 1777, Braunschweig – † 23. február 1855, Göttingen) bol jeden z najväčších matematikov a fyzikov všetkých čias. Zaoberal sa teóriou čísel, matematickou analýzou, geometriou, geodéziou, magnetizmom, astronómiou a optikou.

C. F. Gauss sa narodil ako syn murára a vodného majstra. Počítať vraj vedel skôr ako dobre hovoriť. Čítať sa naučil skoro sám. Keď mal Carl tri roky, stalo sa, že opravil zle spočítanú výplatu. Ale najslávnejšia historka z jeho detstva hovorí o tom, že ako deväťročný školák dokázal za niekoľko sekúnd správne spočítať súčet všetkých čísel od jedna do sto; a pritom odvodiť všeobecný postup pre súčet aritmetického radu. Keď to videl jeho učiteľ, hneď mu zohnal učebnicu matematiky.

40 2006

Trigonometria (z gréčtiny trigona = tri uhly a metro = merať) je disciplína matematiky zaoberajúca sa uhlami, trojuholníkmi a trigonometrickými funkciami ako sínus, kosínus a tangens. Trigonometria má blízky vzťah ku geometrii, aj keď nepanuje všeobecná dohoda aký presne; pre niektorých je trigonometria len pododbor geometrie.

Počiatky trigonometrie sa datujú až ku kultúram starovekého Egyptu a civilizáciam Babylončanov a údolia rieky Indus pred 3000 rokmi. Indickí matematici mali na dobrej úrovni rozvinuté algebraické výpočty s premennými, ktoré využívali v astronómii a medzi ktoré patrila aj trigonometria.

Grécky matematik Hipparchos z Nikaie okolo roku 150 pred Kr. napísal trigonometrické tabuľky pre riešenie problémov s trojuholníkmi.

Iný grécky matematik, Ptolemaios, okolo roku 100 ďalej rozvinul trigonometrický aparát.

41 2006

V matematike sa pod pojmom guľa obvykle rozumie teleso v trojrozmernom Euklidovskom priestore ohraničené sférickou plochou, t. j. plochou, ktorej body sú rovnako vzdialené od pevného bodu (tzv. stred gule). V širšom význame môže guľa znamenať množinu bodov v metrickom priestore, ktoré sú vzdialené od pevného bodu menej než nejaké pevne dané číslo.

Rozlišujeme guľu otvorenú (t. j. povrch tam nepatrí) a uzavrenú (t. j. povrch tam patrí).

V topológii znamená n-rozmerná guľa (obvykle sa značí $B_{n}$ ) topologický priestor, ktorý je homeomorfný s n-rozmernou guľou v Euklidovskom priestore $\mathbb {R} ^{n}$ . V takomto širšom zmysle sa niekedy hovorí, že zem je guľa (ak keď je trochu zdeformovaná v porovnaní s presne Euklidovskou guľou).

42 2006

Euklidovská geometria je matematická teória, ktorej základy položil grécky matematik Euklides z Alexandrie. Euklidove zväzky Základy boli prvou systematickou diskusiou geometrie. Bol to jeden z najvplyvnejších súborov kníh v histórii, tak kvôli jeho metóde, ako aj matematickému obsahu. Metóda pozostáva z predpokladu niekoľkých intuitívne platných axiómov a dôkazu množstva iných tvrdení (viet) z týchto axiómov. Aj keď veľa z Euklidových výsledkov bolo známych gréckym mamematikom pred ním, Euklid bol prvý, ktorý ukázal ako tieto tvrdenia tvoria spolu komplexný deduktívny systém.

43 2006

Bernard Bolzano (* 5. október 1781, Praha – † 18. december 1848, Praha) bol významný nemecky hovoriaci český matematik a filozof.

Bernard Bolzano vyštudoval piaristické gymnázium v Prahe, ktoré ukončil s výborným prospechom roku 1796. Potom sa venoval štúdiu matematiky a logiky v trojročnej filozofickej prípravke, kde prednášal Stanislav Vydra. Školský rok 1799 – 1800 súkromne študoval najmä matematiku a filozofiu a súčasne navštevoval prednášky prvného a druhého ročníka na Filozofickej fakulte Karlo–Ferdinandovej univerzity, a to najmä prednášky matematiky Františka Josef Gerstnera. Napriek obrovskému záujmu o matematiku a filozofiu sa po uplynutí tohto roka rozhodol pre štúdium teológie. Na jeseň roku 1804 sa Bernard Bolzano zaujímal o miesto profesora matematiky na pražskej univerzite, ktoré sa uvoľnilo po odchode S. Vydry do dôchodku. Aj keď na konkurznej skúške, ktorá bola na to miesto vypísaná, obstál veľmi dobre, bolo miesto pridelené staršiemu uchádzačovi, L. Janderovi. Bernard Bolzano sa stal kňazom a na univerzitu nastúpil o rok neskôr, v roku 1805, keď prijal miesto univerzitného učiteľa náboženstva. V tom istom roku získal aj titul doktora filozofie. V roku 1819 mu bolo znemožnené učiť a rok potom bol z učiteľského úradu z rozhodnutia cisára pre svoje reformátorské názory prepustený.

44 2006

Pojem prirodzené číslo môže znamenať buď kladné celé číslo (1, 2, 3,...) alebo nezáporné celé číslo (0, 1, 2, 3,...). Prirodzené čísla majú dve hlavné použitia: počítanie ("na stole sú 3 jablká") alebo poradie ("toto je 3. najväčšie mesto na Slovensku"). Vlastnosti prirodzených čísel súvisiace s deliteľnosťou (ako napr. rozdelenie prvočísel) študuje teória čísel. Problémy, s ktorými sa stretávame pri počítaní (ako napr. Ramseyova teória), študuje kombinatorika. (Pozn.: Horeuvedený význam prirodzených čísel nie matematická definícia, pretože zvyčajne všetky ostatné čísla sa definujú pomocou prirodzených, čo by viedlo k definícii kruhom. Korektné matematické definície sú uvedené nižšie.)

45 2006

Kombinatorika (alebo aj kombinatorická matematika čí kombinatorická analýza) je súčasť diskrétnej matematiky, ktorá študuje (spravidla) konečné množiny objektov, ktoré vyhovujú zadaným kritériám a zaoberá sa najmä "počítaním" objektov v týchto množinách (enumeratívna kombinatorika) a rozhodovaním, či isté "optimálne" objekty a množiny objektov vôbec existujú (extremálna kombinatorika). Jedným z najvýznamejších kombinatorikov nedávnej doby bol Gian-Carlo Rota, ktorý pomohol sformalizovať kombinatoriku ako takú začiatkom šesťdesiatych rokov. Produktívny riešiteľ rôznych problémov Paul Erdös pracoval hlavne na extremálnych problémoch.

Typický príklad, na ktorý sa kombinatorika snaží nájsť odpoveď, je takýto: Aký je počet všetkých usporiadaní balíka 52 hracích kariet? Odpoveď je 52! (t. j. "päťdesiatdva faktoriál"), čo je súčin všetkých prirodzených čísel od jedna po 52. Je možno prekvapujúce, že toto číslo, približne 8.065817517094 × 10⁶⁷, je tak veľké. Je to o niečo viac než 8, za ktorou nasleduje 67 núl. Pri porovnaní s inými veľkými číslami je väčšie než druhá mocnina Avogadrovej konštanty (6.022 × 10²³), ktorá vyjadruje počet častíc v jednom mole látky.

46 2006

Teória zložitosti je časť teoretickej informatiky zaoberajúca sa množstvom požadovaných zdrojov počas výpočtu riešiaceho daný problém. Najčastejšie uvažovaným zdrojom je čas (koľko krokov je potrebných na vyriešenie problému) a priestor (koľko pamäti je potrebnej na vyriešenie problému). Príklady ďalších zdrojov sú počet paralelných procesorov a celková práca vynaložená na riešenie problému v paralelnom systéme. Teória zložitosti sa odlišuje od teórie vypočítateľnosti, ktorá skúma len či sa problém dá vyriešiť alebo nie, bez uvažovania o potrebných zdrojoch.

Po založení teórie objasňujúcej, ktoré problémy sa dajú algoritmicky riešiť a ktoré nie, bolo prirodzené sa pýtať na relatívnu výpočtovú zložitosť vypočítateľných funkcií.

Na problémy sa pozeráme ako na formálne jazyky, a tak jeden "problém" je často celá množina otázok, kde každá otázka je slovo konečnej dĺžky z tohto jazyka. Napríklad, problém FAKTORIZÁCIA je špecifikovaný nasledovne: na vstupe je dané celé číslo zapísané v binárnom tvare, na výstupe požaduje všetky prvočíselné faktory tohto čísla. Jedna takáto otázka (teda konkrétne jedno slovo z jazyka) sa nazýva inštancia problému; napr. "vráť všetky prvočíselné faktory čísla 15" je jedna inštancia problému FAKTORIZÁCIA.

47 2006

Teória zložitosti je časť teoretickej informatiky zaoberajúca sa množstvom požadovaných zdrojov počas výpočtu riešiaceho daný problém. Najčastejšie uvažovaným zdrojom je čas (koľko krokov je potrebných na vyriešenie problému) a priestor (koľko pamäti je potrebnej na vyriešenie problému). Príklady ďalších zdrojov sú počet paralelných procesorov a celková práca vynaložená na riešenie problému v paralelnom systéme. Teória zložitosti sa odlišuje od teórie vypočítateľnosti, ktorá skúma len či sa problém dá vyriešiť alebo nie, bez uvažovania o potrebných zdrojoch.

Po založení teórie objasňujúcej, ktoré problémy sa dajú algoritmicky riešiť a ktoré nie, bolo prirodzené sa pýtať na relatívnu výpočtovú zložitosť vypočítateľných funkcií.

Na problémy sa pozeráme ako na formálne jazyky, a tak jeden "problém" je často celá množina otázok, kde každá otázka je slovo konečnej dĺžky z tohto jazyka. Napríklad, problém FAKTORIZÁCIA je špecifikovaný nasledovne: na vstupe je dané celé číslo zapísané v binárnom tvare, na výstupe požaduje všetky prvočíselné faktory tohto čísla. Jedna takáto otázka (teda konkrétne jedno slovo z jazyka) sa nazýva inštancia problému; napr. "vráť všetky prvočíselné faktory čísla 15" je jedna inštancia problému FAKTORIZÁCIA.

48 2006

Teória zložitosti je časť teoretickej informatiky zaoberajúca sa množstvom požadovaných zdrojov počas výpočtu riešiaceho daný problém. Najčastejšie uvažovaným zdrojom je čas (koľko krokov je potrebných na vyriešenie problému) a priestor (koľko pamäti je potrebnej na vyriešenie problému). Príklady ďalších zdrojov sú počet paralelných procesorov a celková práca vynaložená na riešenie problému v paralelnom systéme. Teória zložitosti sa odlišuje od teórie vypočítateľnosti, ktorá skúma len či sa problém dá vyriešiť alebo nie, bez uvažovania o potrebných zdrojoch.

Po založení teórie objasňujúcej, ktoré problémy sa dajú algoritmicky riešiť a ktoré nie, bolo prirodzené sa pýtať na relatívnu výpočtovú zložitosť vypočítateľných funkcií.

Na problémy sa pozeráme ako na formálne jazyky, a tak jeden "problém" je často celá množina otázok, kde každá otázka je slovo konečnej dĺžky z tohto jazyka. Napríklad, problém FAKTORIZÁCIA je špecifikovaný nasledovne: na vstupe je dané celé číslo zapísané v binárnom tvare, na výstupe požaduje všetky prvočíselné faktory tohto čísla. Jedna takáto otázka (teda konkrétne jedno slovo z jazyka) sa nazýva inštancia problému; napr. "vráť všetky prvočíselné faktory čísla 15" je jedna inštancia problému FAKTORIZÁCIA.

49 2006

Niels Henrik Abel (* 5. august 1802 – † 6. apríl 1829), nórsky matematik, narodil sa v meste Finnøy. V roku 1815 nastúpil na katedrálnu školu v Christianii (terajšie Oslo). Už po troch rokoch dal najavo svojho matematického génia brilantnými riešeniami originálnych problémov od Bernta Holmboea. Zhruba v tom čase jeho otec, chudobný protestantský duchovný, zomrel a jeho rodina sa ocitla v stiesnených finančných pomeroch, ale malý dôchodok od štátu dovolil Abelovi nastúpiť na Chistianskú univerzitu v roku 1821.