Sínus

Graf funkcie sínus

O iných významoch výrazu Sínus pozri Sínus (rozlišovacia stránka).

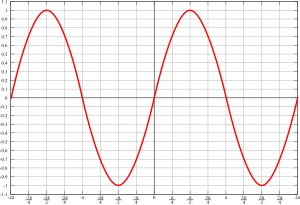
Sínus patrí medzi goniometrické funkcie. V pravouhlom trojuholníku je definovaný ako pomer dĺžky protiľahlej odvesny k uhlu a dĺžky prepony trojuholníka. Graf funkcie sínus sa nazýva sínusoida alebo sínusovka.

Pôvod slova

Latinské slovo „Sinus“ znamená „ohyb, zakrivenie, alebo prsia“. V tomto význame bolo slovo prevzaté od arabských matematikov, ktorí si slovo „jiba“ (جيب) „vrecko, záhyb látky“ požičali od indických matematikov (Sanskrit „jiva“ ‘tetiva‘ - odvodené od zakriveného priebehu vlákna, ktoré je navinuté na palici vo forme závitu.).

Vlastnosti

Funkcia $y=\sin x\,\!$ má nasledujúce vlastnosti (kde k je ľubovoľné celé číslo):

• Definičný obor: $\mathbb{R}$ (reálne čísla)
• Obor hodnôt: $\langle-1;1\rangle$
• Funkcia je rastúca: v každom intervale $\langle-\frac{\pi}{2}+2k\pi; \frac{\pi}{2}+2k\pi\rangle$
• Funkcia je klesajúca: v každom intervale $\langle\frac{\pi}{2}+2k\pi; -\frac{\pi}{2}+2(k+1)\pi\rangle$
• Funkcia nadobúda maximum rovné 1 v bode: $\frac{\pi}{2}+2k\pi$
• Funkcia nadobúda minimum rovné -1 v bode: $-\frac{\pi}{2}+2k\pi$
• Derivácia funkcie: $y'=\cos x\,\!$
• Integrál: $\int \sin x\, \mathrm{d}x = -\cos x + c$
• Taylorov rad: $\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}$, rovnosť platí pre všetky reálne čísla
• Inverzná funkcia: arkus sínus (arcsin), je to inverzná funkcia k funkcii sínus zúženej na interval $[-\pi/2,+\pi/2]$
• Sínus je funkcia:
  • nepárna
  • ohraničená zhora i zdola
  • periodická s periódou $2\pi$

Sínus v komplexnom obore

Funkcia sínus je v komplexných číslach definovaná súčtom radu

$\sin z = z - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \ldots = \sum_{n=0}^\infty \frac{(-1)^nz^{2n+1}}{(2n+1)!},$

ktorý konverguje na celej komplexnej rovine. Pre každé dve komplexné čísla z₁,z₂ platí:

$\sin z = \frac{e^{iz}-e^{-iz}}{2i},$

$\sin\left(z_1+z_2\right)=\sin z_1 \cos z_2 + \cos z_1 \sin z_2,$

$\sin iz = i \sinh z,\,$

Tieto vzorce vyplývajú priamo z príslušných definičných mocninových radov daných funkciou. Sínus je na celej komplexnej rovine jednoznačná holomorfná funkcia.

Sínus ako riešenie diferenciálnej rovnice

Niekedy je výhodné definovať funkciu sínus ako riešenie Cauchyho úlohy

$y''(x)+y(x)=0,\ y(0)=0, y'(0)=1.$

Pozri aj

• Sínusová veta

Iné projekty

Commons

• Commons ponúka multimediálne súbory na tému Sínus